СОДЕРЖАНИЕ ВВЕДЕНИЕ *
МНОЖЕСТВО
ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА В
СФЕРА
НЕКОТОРЫЕ СВОЙСТВА СФЕРЫ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ *
Многие величины, представляющие интерес, зависят не от одного, а от очень многих факторов, и если сама величина и каждый из определяющих его факторов могут быть охарактеризованы некоторым числом, то указанная зависимость сводится к тому, что упорядоченному набору
Например, площадь прямоугольника есть произведение длин его сторон; объём данного количества газа вычисляется по формуле
где
Мы ставим себе целью научиться исследовать функции многих переменных так же, как мы научились исследовать функции одного переменного. Как и в случае функции одного переменного, изучение функции многих числовых переменных начинается с описания их области определения.
Условимся через
Каждый такой набор будем обозначать одной буквой
Число
Геометрические аналогии можно продолжить и ввести на множестве
Функция
определяемая формулой (1), очевидно, обладает следующими свойствами:
Последнее неравенство (называемое опять-таки по геометрической аналогии неравенством треугольника) есть частный случай неравенства Минковского.
Функцию, определённую на парах
Множество
Таким образом, мы превратили
Из соотношения (1) следует, что при
т. е. расстояние между точками
Из (2), как и из (1), видно, что при
ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА В
Определение 1. При
называется шаром с центром
Определение 2. Множество
Пример 1.
Пример 2.
Пример 3. Шар
Действительно, если
Пример 4. Множество
Определение 3. Множество
Пример 5. Множество
Сфера – множество
Сфера
в частности,
Уравнение сферы
(здесь
Положение какой-либо точки в пространстве относительно сферы характеризуется степенью точки. Совокупность всех сфер, относительно которых данная точка имеет одинаковую степень, составляет сеть сферы. Совокупность всех сфер, относительно которых точки некоторой прямой (радикальной оси) имеют одинаковую степень (различную для различных точек), составляет пучок сферы.
С точки зрения дифференциальной геометрии, сфера
Некоторые из таких свойств, принятые за основные, послужили отправной точкой для обобщения понятия сферы. Так, например, аффинная сфера определяется тем, что все её (аффинные) нормали пересекаются в одной точке; псевдосфера – поверхность в
На сферу
С точки зрения (дифференциальной) топологии, сфера
Группы гомологий сферы
в частности
Группы гомотетий сферы
Например,
И здесь понятие сфера получает обобщение. Например, дикая сфера – топологическая сфера в
Топологическое пространство, гомеоморфное сфере, называется топологической сферой. Одним из основных здесь является вопрос об условиях того, что некоторое пространство является топологической сферой. Примеры.
а) Инвариантная топологическая характеристика сферы
б) Полное односвязное риманово пространство размерности
в) Односвязное замкнутое гладкое многообразие, (целые) гомологии которого совпадают с гомологиями
Совершенно аналогично определяется сфера
В нормированном пространстве
другое определение:
Приложения понятия сфера чрезвычайно разнообразны. Например сферы участвуют в конструкциях новых пространств или дополнительных структур на них. Так, например, проективные пространства
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
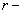 ,
,
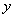 (1)
(1)
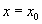 ,
,
 Главная
Главная