Вычисление кратных интегралов методом ячеек с автоматическим выбором шага
Содержание 1 Постановка задачи 2 Теоретическая часть 2.1 Понятие о кубатурных формулах 2.2 Метод ячеек 3 2.3 Последовательное интегрирование 2.4 Кубатурная формула типа Симпсона 2.5 Принципы построения программ с автоматическим выбором шага 3 Список использованной литературы 4 Практическая часть 4.1 Решение задачи 4.2 Блок-схема программы 4.3 Листинг программы 4.4 Результаты решения 1 Постановка задачи
Найти при помощи метода ячеек значение интеграла , где
2 Теоретическая часть Рассмотрим K-мерный интеграл вида:
где
2.1 Понятие о кубатурных формулах Кубатурные формулы или, иначе формулы численных кубатур предназначены для численного вычисления кратных интегралов.
Пусть функция
Чтобы найти коэффициенты
степень которых не превышает заданного числа
Таким образом, коэффициенты
Для того чтобы система (4) была определённой, необходимо, чтобы число неизвестных
2.2 Метод ячеек
Рассмотрим K-мерный интеграл по пространственному параллелепипеду
Для повышения точности можно разбить область на прямоугольные ячейки (рис. 2). Приближённо вычисляя интеграл в каждой ячейке по формуле средних и обозначая через
Справа стоит интегральная сумма; следовательно, для любой непрерывной
Оценим погрешность интегрирования. Формула (5) по самому её выводу точна для
где
ибо все члены разложения, нечётные относительно центра симметрии ячейки, взаимно уничтожаются. Пусть в обобщённой квадратурной формуле (6) стороны пространственного параллелепипеда разбиты соответственно на N 1 , N 2 , …, N k равных частей. Тогда погрешность интегрирования (8) для единичной ячейки равна:
Суммируя это выражение по всем ячейкам, получим погрешность обобщённой формулы:
т.е. формула имеет второй порядок точности. При этом, как и для одного измерения, можно применять метод Рунге–Ромберга, но при одном дополнительном ограничении: сетки по каждой переменной сгущаются в одинаковое число раз.
Обобщим формулу ячеек на более сложные области. Рассмотрим случай K=2. Легко сообразить, что для линейной функции
Разумеется, практическую ценность это имеет только для областей простой формы, где площадь и центр тяжести легко определяется; например, для треугольника, правильного многоугольника, трапеции. Но это значит, что обобщённую формулу (6) можно применять к областям, ограниченным ломаной линией, ибо такую область всегда можно разбить на прямоугольники и треугольники.
Для области с произвольной границей формулу (6) применяют иным способом. Наложим на область
Оценим погрешность формулы (6). В каждой внутренней ячейке ошибка составляет
Вычисление объёма граничной ячейки довольно трудоёмко, ибо требует определения положения границы внутри ячейки. Можно вычислять интегралы по граничным ячейкам более грубо или вообще не включать их в сумму (6). Погрешность при этом будет
Мы видели, что к области произвольной формы метод ячеек трудно применять; поэтому всегда желательно заменой переменных преобразовать область интегрирования в прямоугольный параллелепипед (это относится практически ко всем методам вычисления кратных интегралов). 2.3 Последовательное интегрирование Снова рассмотрим интеграл по K-мерной области, разбитой сеткой на ячейки (рис. 2). Его можно вычислить последовательным интегрированием:
Каждый однократный интеграл легко вычисляется на данной сетке по квадратурным формулам типа:
Последовательное интегрирование по всем направлениям приводит к кубатурным формулам, которые являются прямым произведением одномерных квадратурных формул:
Например, при K=2, если по каждому направлению выбрана обобщённая формула трапеций, а сетка равномерная, то веса кубатурной формулы равны
Вообще говоря, для разных направлений можно использовать квадратурные формулы разных порядков точности
Желательно для всех направлений использовать квадратурные формулы одинакового порядка точности. Можно подобрать веса и положение линий сетки так, чтобы одномерная квадратурная формула была точна для многочлена максимальной степени, т.е. была бы формулой Гаусса, тогда, для случая K=2:
где –нули многочленов Лежандра и соответствующие веса. Эти формулы рассчитаны на функции высокой гладкости и дают для них большую экономию в числе узлов по сравнению с более простыми формулами.
Произвольная область. Метод последовательного интегрирования можно применять к области произвольной формы, например, с криволинейной границей. Рассмотрим этот случай при K=2. Для этого проведём через область хорды, параллельные оси
Сначала вычислим интеграл по
При вычислении интеграла по
Тогда второе интегрирование выполняется по формулам Гаусса–Кристоффеля:
где
Чтобы можно было применять эту формулу, надо ординаты хорд на рис. 4 заранее выбрать в соответствии с узлами (13). Если это не было сделано, то придётся ограничиться интегрированием
2.4 Кубатурная формула типа Симпсона
Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед
Всего таким образом, получим
Находим K-мерный интеграл, вычисляя каждый внутренний интеграл по квадратурной формуле Симпсона на соответствующем отрезке. Проведём полностью все вычисления для случая K=2:
Применяя к каждому интегралу снова формулу Симпсона, получим:
или
Формулу (15) будем называть кубатурной формулой Симпсона . Следовательно,
где
Если размеры пространственного параллелепипеда
Опять рассмотрим случай K=2. Положим, что стороны прямоугольника
Пусть
и
Для сокращения введём обозначение
Применяя формулу (15) к каждому из прямоугольников крупной сети, будем иметь (рис.6):
Отсюда, делая приведение подобных членов, окончательно находим:
где коэффициенты
Если область интегрирования
В таком случае, очевидно, имеем:
Последний интеграл приближённо может быть вычислен по общей кубатурной формуле (16). 2.5 Принципы построения программ с автоматическим выбором шага При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако в случае резко меняющихся функций возникают некоторые проблемы. Если первоначальная сетка, на которой исследуется подынтегральная функция, частая, то сильно загружается память ЭВМ; если она редкая, то не удаётся хорошо аппроксимировать оптимальное распределение узлов на участках резкого изменения подынтегральной функции. Рассмотрим некоторые из процедур распределения узлов интегрирования, обеспечивающие лучшее приближение к оптимальному распределению узлов для функций с особенностями.
Пусть на элементарном отрезке интегрирования
Процедура должна также иметь блок окончания работы: если оказалось, что
Другая процедура, которую можно назвать
вертикальной
, определяется заданием числа
3 Список использованной литературы. 1. Бахвалов Н.С. Численные методы. т.1 – М.: Наука. 1975. 2. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966. 3. Калиткин Н.Н Численные методы. – М.: Наука, 1978. 4. Мусіяка В.Г. Основи чисельних методів механіки. – Дніпропетровськ: Видавництво ДДУ, 1993. 4 Практическая часть 4.1 Решение задачи
Наложим на область G прямоугольную сетку с шагами
Не учитывая граничные ячейки, получаем:
Дополнение от граничных ячеек:
Окончательно получаем:
4.4 Результаты решения Расчёт проводился при точности eps=1E-6. Интеграл равен: 0.221612 Количество ячеек равно 8525. Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
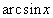 –
область, ограниченная функциями
–
область, ограниченная функциями
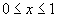 .
.
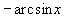 (1)
(1)
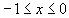 - некоторая K-мерная точка. Далее для простоты все рисунки будут сделаны для случая K=2.
- некоторая K-мерная точка. Далее для простоты все рисунки будут сделаны для случая K=2.
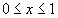 определена и непрерывна в некоторой ограниченной области
определена и непрерывна в некоторой ограниченной области
 . В этой области
. В этой области
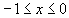 . Для вычисления интеграла
. Для вычисления интеграла
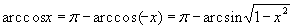 приближённо полагают:
приближённо полагают:
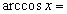 (2)
(2)
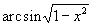 , потребуем точного выполнения кубатурной формулы (2) для всех полиномов
, потребуем точного выполнения кубатурной формулы (2) для всех полиномов
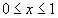 (3)
(3)
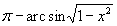 . Для этого необходимо и достаточно, чтобы формула (2) была точной для произведения степеней
. Для этого необходимо и достаточно, чтобы формула (2) была точной для произведения степеней
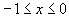 . Полагая в (1)
. Полагая в (1)
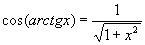 , будем иметь:
, будем иметь:
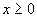 (4)
(4)
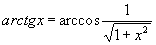 формулы (2), вообще говоря, могут быть определены из системы линейных уравнений (4).
формулы (2), вообще говоря, могут быть определены из системы линейных уравнений (4).
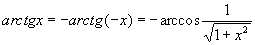 было равно числу уравнений. В случае
было равно числу уравнений. В случае
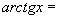 получаем:
получаем:
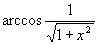
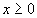 . По аналогии с формулой средних можно приближённо заменить функцию на её значение в центральной точке параллелепипеда. Тогда интеграл легко вычисляется:
. По аналогии с формулой средних можно приближённо заменить функцию на её значение в центральной точке параллелепипеда. Тогда интеграл легко вычисляется:
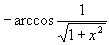 (5)
(5)
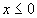 соответственно площадь ячейки и координаты её центра, получим:
соответственно площадь ячейки и координаты её центра, получим:
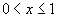 (6)
(6)
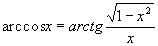 она сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю.
она сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю.
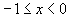 . Но непосредственной подстановкой легко убедиться, что формула точна и для любой линейной функции. В самом деле, разложим функцию по формуле Тейлора:
. Но непосредственной подстановкой легко убедиться, что формула точна и для любой линейной функции. В самом деле, разложим функцию по формуле Тейлора:
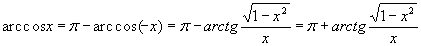 (7)
(7)
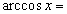 , а все производные берутся в центре ячейки. Подставляя это разложение в правую и левую части квадратурной формулы (5) и сравнивая их, аналогично одномерному случаю легко получим выражение погрешности этой формулы:
, а все производные берутся в центре ячейки. Подставляя это разложение в правую и левую части квадратурной формулы (5) и сравнивая их, аналогично одномерному случаю легко получим выражение погрешности этой формулы:
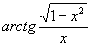 (8)
(8)
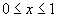
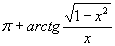 (9)
(9)
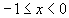 формула типа (5) будет точна в области произвольной формы, если под S подразумевать площадь области, а под
формула типа (5) будет точна в области произвольной формы, если под S подразумевать площадь области, а под
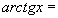 –координаты центра тяжести, вычисляемые по обычным формулам:
–координаты центра тяжести, вычисляемые по обычным формулам:
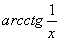 (10)
(10)
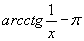 сетку из K-мерных параллелепипедов (рис.3). Те ячейки сетки, все точки которых принадлежат области, назовём
внутренними
; если часть точек ячейки принадлежит области, а часть – нет, то назовём ячейку
граничной
. Объём внутренней ячейки равен произведению её сторон. Объёмом граничной ячейки будем считать объем той её части, которая попадает внутрь
сетку из K-мерных параллелепипедов (рис.3). Те ячейки сетки, все точки которых принадлежат области, назовём
внутренними
; если часть точек ячейки принадлежит области, а часть – нет, то назовём ячейку
граничной
. Объём внутренней ячейки равен произведению её сторон. Объёмом граничной ячейки будем считать объем той её части, которая попадает внутрь
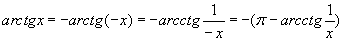 ; этот объём вычислим приближённо. Эти площади подставим в (6) и вычислим интеграл.
; этот объём вычислим приближённо. Эти площади подставим в (6) и вычислим интеграл.
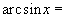 по отношению к значению интеграла по данной ячейке. В каждой граничной ячейке относительная ошибка есть
по отношению к значению интеграла по данной ячейке. В каждой граничной ячейке относительная ошибка есть
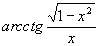 , ибо центр ячейки не совпадает с центром тяжести входящей в интеграл части. Но самих граничных ячеек примерно в
, ибо центр ячейки не совпадает с центром тяжести входящей в интеграл части. Но самих граничных ячеек примерно в
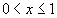 раз меньше, чем внутренних. Поэтому при суммировании по ячейкам общая погрешность будет
раз меньше, чем внутренних. Поэтому при суммировании по ячейкам общая погрешность будет
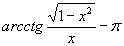 , если функция дважды непрерывно дифференцируема; это означает второй порядок точности.
, если функция дважды непрерывно дифференцируема; это означает второй порядок точности.
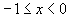 , и для хорошей точности потребуется более подробная сетка.
, и для хорошей точности потребуется более подробная сетка.
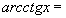
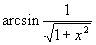
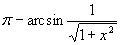 (11)
(11)
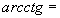 соответственно для внутренних, граничных и угловых узлов сетки. Легко показать, что для дважды непрерывно дифференцируемых функций эта формула имеет второй порядок точности, и к ней применим метод Рунге–Ромберга.
соответственно для внутренних, граничных и угловых узлов сетки. Легко показать, что для дважды непрерывно дифференцируемых функций эта формула имеет второй порядок точности, и к ней применим метод Рунге–Ромберга.
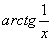 . Тогда главный член погрешности имеет вид:
. Тогда главный член погрешности имеет вид:
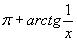
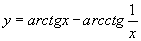 (12)
(12)
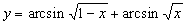 , и на них введём узлы, расположенные на каждой хорде так, как нам требуется (рис. 4). Представим интеграл в виде:
, и на них введём узлы, расположенные на каждой хорде так, как нам требуется (рис. 4). Представим интеграл в виде:
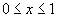
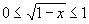 вдоль каждой хорды по какой-нибудь одномерной квадратурной формуле, используя введённые узлы. Затем вычислим интеграл по
вдоль каждой хорды по какой-нибудь одномерной квадратурной формуле, используя введённые узлы. Затем вычислим интеграл по
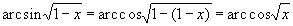 ; здесь узлами будут служить проекции хорд на ось ординат.
; здесь узлами будут служить проекции хорд на ось ординат.
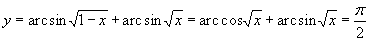 имеется одна тонкость. Если область ограничена гладкой кривой, то при
имеется одна тонкость. Если область ограничена гладкой кривой, то при
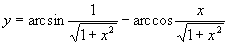 длина хорды стремится к нулю не линейно, а как
длина хорды стремится к нулю не линейно, а как
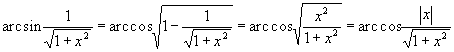 ; значит, вблизи этой точки
; значит, вблизи этой точки
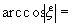 . То же будет при
. То же будет при
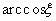 . Поэтому интегрировать непосредственно
. Поэтому интегрировать непосредственно
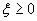 по формулам высокого порядка точности бессмысленно. Целесообразно выделить из
по формулам высокого порядка точности бессмысленно. Целесообразно выделить из
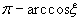 основную особенность в виде веса
основную особенность в виде веса
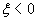 , которому соответствуют ортогональные многочлены Чебышева второго рода.
, которому соответствуют ортогональные многочлены Чебышева второго рода.
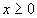 (13)
(13)
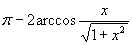 , а
, а
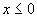 и
и
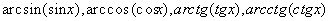 –нули и веса многочленов Чебышева второго рода.
–нули и веса многочленов Чебышева второго рода.
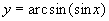 по обобщённой формуле трапеций, причём её эффективный порядок точности в этом случае будет ниже второго.
по обобщённой формуле трапеций, причём её эффективный порядок точности в этом случае будет ниже второго.
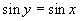 (рис. 5), стороны которого параллельны осям координат. Каждый из промежутков
(рис. 5), стороны которого параллельны осям координат. Каждый из промежутков
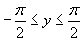 разобьём пополам точками:
разобьём пополам точками:
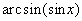 , где
, где
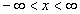 .
.
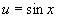 точек сетки. Имеем:
точек сетки. Имеем:
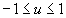 (14)
(14)
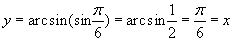
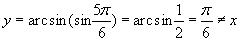
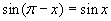 (15)
(15)
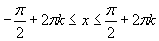 (15ў
)
(15ў
)
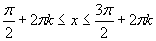 – сумма значений подынтегральной
функции в вершинах прямоугольника
– сумма значений подынтегральной
функции в вершинах прямоугольника
 ,
,
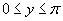 –
сумма значений в серединах сторон прямоугольника
–
сумма значений в серединах сторон прямоугольника
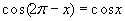 ,
,
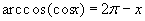 – значение функции
– значение функции
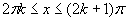 в центре
прямоугольника
в центре
прямоугольника
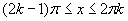 . Кратности этих значений обозначены
на рис. 5.
. Кратности этих значений обозначены
на рис. 5.
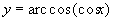 велики,
то для увеличения точности кубатурной формулы область разбивают на систему параллелепипедов,
к каждому из которых применяют кубатурную формулу Симпсона.
велики,
то для увеличения точности кубатурной формулы область разбивают на систему параллелепипедов,
к каждому из которых применяют кубатурную формулу Симпсона.
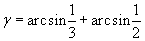 мы разделили соответственно на
мы разделили соответственно на
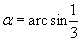 и
и
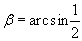 равных частей; в результате получилась относительно крупная сеть
равных частей; в результате получилась относительно крупная сеть
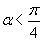 прямоугольников (на рис. 6 вершины этих прямоугольников отмечены более крупными кружками). Каждый из этих прямоугольников в свою очередь разделим на четыре равные части. Вершины этой последней мелкой сети прямоугольников примем за узлы
прямоугольников (на рис. 6 вершины этих прямоугольников отмечены более крупными кружками). Каждый из этих прямоугольников в свою очередь разделим на четыре равные части. Вершины этой последней мелкой сети прямоугольников примем за узлы
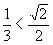 кубатурной формулы.
кубатурной формулы.
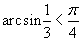 и
и
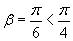 . Тогда сеть узлов будет иметь следующие координаты:
. Тогда сеть узлов будет иметь следующие координаты:
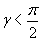
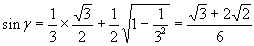
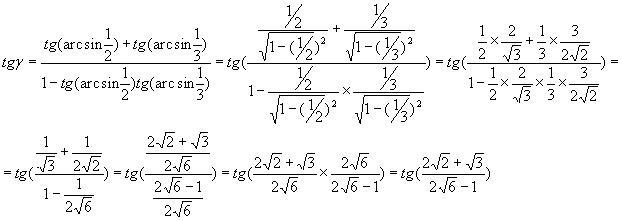
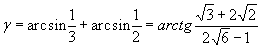 (16)
(16)
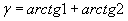 являются соответствующими элементами матрицы
являются соответствующими элементами матрицы
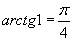
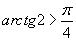 – произвольная, то строим параллелепипед
– произвольная, то строим параллелепипед
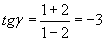 , стороны которого параллельны осям координат (рис. 83). Рассмотрим вспомогательную функцию
, стороны которого параллельны осям координат (рис. 83). Рассмотрим вспомогательную функцию
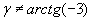
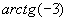
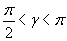 вычисляется приближённое значение интеграла
вычисляется приближённое значение интеграла
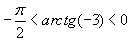 и мера погрешности
и мера погрешности
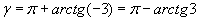 . Требуется вычислить
. Требуется вычислить
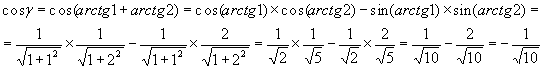 . Первая процедура, которую естественно назвать
горизонтальной
, определяется заданием параметров
. Первая процедура, которую естественно назвать
горизонтальной
, определяется заданием параметров
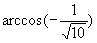 . Полагаем
. Полагаем
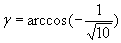 . Предположим, что каким-то образом уже вычислено приближённое значение интеграла
. Предположим, что каким-то образом уже вычислено приближённое значение интеграла
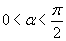 . Программа располагает в каждый момент времени некоторым значением
. Программа располагает в каждый момент времени некоторым значением
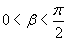 , с которым надо начинать считать оставшуюся часть интеграла. Вычисляем величину
, с которым надо начинать считать оставшуюся часть интеграла. Вычисляем величину
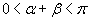 , соответствующую отрезку
, соответствующую отрезку
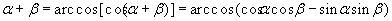 . Если оказалось
. Если оказалось
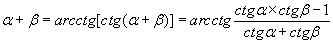 , то вычисляем приближённое значение
, то вычисляем приближённое значение
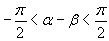 и полагаем
и полагаем
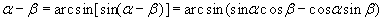 . Мы получили приближённое значение величины
. Мы получили приближённое значение величины
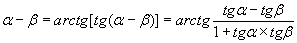 . В случае
. В случае
 полагаем
полагаем
 , в противном случае полагаем
, в противном случае полагаем
 . Мы готовы к следующему шагу. Если оказалось
. Мы готовы к следующему шагу. Если оказалось
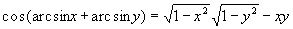 , то принимаем
, то принимаем
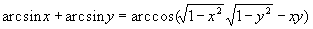 за новое значение величины
за новое значение величины
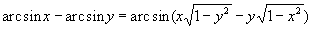 и возвращаемся к исходной позиции: вычислено значение интеграла
и возвращаемся к исходной позиции: вычислено значение интеграла
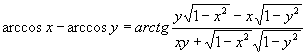 и задан шаг
и задан шаг
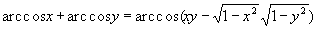 . Начальные условия для применения процедуры:
. Начальные условия для применения процедуры:
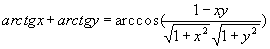
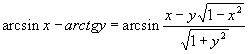 , то следует положить
, то следует положить
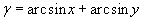 . Установилась практика брать
. Установилась практика брать
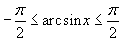 .
.
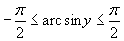 и заключается в следующем. Пусть на каком-то шаге возникает необходимость вычисления интеграла по отрезку разбиения
и заключается в следующем. Пусть на каком-то шаге возникает необходимость вычисления интеграла по отрезку разбиения
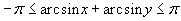 :
:
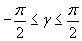 ; вычисляется величина
; вычисляется величина
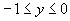 , соответствующая этому отрезку. Если она оказалась меньше
, соответствующая этому отрезку. Если она оказалась меньше
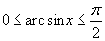 , то этот интеграл вычисляется по соответствующей формуле и программа переходит к следующему справа отрезку разбиения. В противном случае отрезки
, то этот интеграл вычисляется по соответствующей формуле и программа переходит к следующему справа отрезку разбиения. В противном случае отрезки
 и
и
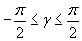 объявляются отрезками разбиения, и программа обращается к вычислению интеграла по левому из этих отрезков. В начале работы программа обращается к вычислению исходного интеграла
объявляются отрезками разбиения, и программа обращается к вычислению интеграла по левому из этих отрезков. В начале работы программа обращается к вычислению исходного интеграла
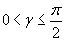 . Некоторым недостатком этой процедуры является необходимость запоминания отрезков разбиения, интегрирование по которым на данный момент не произведено.
. Некоторым недостатком этой процедуры является необходимость запоминания отрезков разбиения, интегрирование по которым на данный момент не произведено.
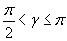 и
и
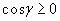 , вследствие чего получим внутреннюю прямоугольную ячейку с площадью
, вследствие чего получим внутреннюю прямоугольную ячейку с площадью
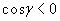 и координатами центра
и координатами центра
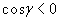 и две граничные треугольные ячейки с площадями и координатами центров соответственно
и две граничные треугольные ячейки с площадями и координатами центров соответственно
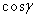 ,
,
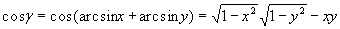 и
и
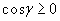 .
.
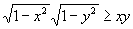 .
.
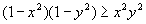 .
.
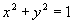
 Главная
Главная