Использование численных методов при решении обратных задач теплопроводности. Введение. Постановка прямых и обратных задач теплообмена. Задачи о теплообмене между окружающей средой и твердым телом или некоторой системой принято рассматривать с позиции соотношения причина—следствие. Цель прямых задач теплообмена представляет собой установление таких причинно - следственных связей. Согласно принятой модели, к причинным характеристикам теплообменного процесса в теле или системе следует отнести начальные условия, теплофизические свойства, внутренние источники тепла и проводимости, граничные условия и их параметры, а также геометрические характеристики тела или системы, тогда то или иное тепловое состояние, определяемое температурным полем исследуемого объекта будет следствием . Обратную задачу теплообмена будем иметь , при такой формулировке проблемы, при которой по определенной информации о температурном поле требуется восстановить причинные характеристики. Так как в отличие от прямых задач, обратные не могут соответствовать реальным событиям: нельзя обратить ход теплообменного процесса и тем более изменить течение времени, постановки обратной задачи являются физически некорректными. При математической формализации физическая некорректность уже проявляется, чаще, например, в неустойчивости решения, как математическая. Таким образом, обратные задачи представляют собой типичный пример некорректно поставленных задач в теории теплообмена. В осстановление тепловых условий на границе тела называют граничной задачей теплообмена. К этому типу задач относят, и задачу, связанную с продолжением решения уравнения теплопроводности от некоторой границы, где одновременно заданы температура Т( х*, т) и плотность теплового потока q( х*, т). Организация охлаждения конструкции камер сгорания.
Одним из важнейших вопросов проектирования является организация охлаждения конструкции камер сгорания. Эта задача усложняется ещё и тем, что тепловые процессы протекают при высоких температурах
Температура камеры, вследствие мощных суммарных конвективных и лучистых тепловых потоков в стенке камеры, может достигать значений превышающих (1000 - 1500
Коэффициент конвективной теплоотдачи от горячих продуктов сгорания к стенкам камеры и конвективные тепловые потоки
С учетом совместного воздействия конвективного и лучистого теплового потоков в соответствующем сечении конструкции узла по значениям параметров (давление, состав и температура продуктов сгорания в ядре газового потока и в пристеночном слое) на установившемся режиме эксплуатации определяется коэффициент теплоотдачи от продуктов сгорания. Задача определения теплового состояния в период работы, в условиях, когда время выхода рассматриваемых конструкций на установившийся тепловой режим соизмеримо и может оказаться даже большим времени их работы при эксплуатации, сводится к расчету прогрева их под воздействием высокотемпературных продуктов сгорания.
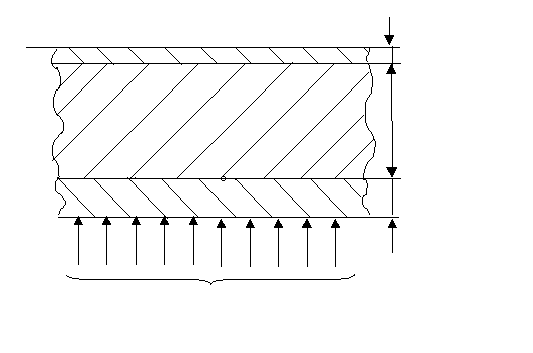
На рисунке 1 один приведена следующая схема корпуса камеры сгорания: на поверхности в сечении располагается по две точки замера, расположенных в диаметрально противоположных точках периметра корпуса. Сечение I - I корпуса сопла можно представить в виде однослойной, неограниченной пластины, а сечение II - II - в виде двухслойной, неограниченной пластины. На рисунках 2, 3 представлены расчетные схемы элементов конструкции.
Обратная тепловая задача нарисованной на рисунке 3 пластины формулируется следующим образом: требуется по замерам температуры
Системы линейных алгебраических уравнений.
Функции
Тогда коэффициенты и свободные члены системы (20) можно представить в виде:
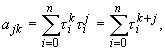 (21)
(21)
, где, так как квадратичная форма
- система линейных алгебраических уравнений где
Существуют прямые и итерационные методы решения таких систем. Методы, основанные на разложении матрицы А в произведении более простых матриц (диагональных, треугольных, ортогональных) называют прямыми методами решения систем линейных алгебраических уравнений. При использовании прямых методов исходная система уравнений (23) распадается на несколько более простых систем, которые решаются последовательно. Потому, как при исключении округлений, то через вполне определенное заранее известное конечное число шагов получится точное решение системы (23), прямые методы называют также точными.
Методы, в которых решение находится как предел при
Метод наименьших квадратов.
Функция
совокупность линейно независимых на
Определим линейную комбинацию этих функций в виде:
(эта
сумма является функцией коэффициентов
при условии, что сумма квадратов ее отклонений от заданных значений
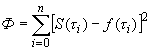 (18)
(18)
былы бы минимальной. Используем для решения задачи приемы дифференциального исчисления.
Найдем частные производные функции
где
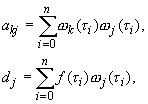
Легко доказать, что если среди точек
Таким образом, метод наименьших квадратов привёл к необходимости решать систему алгебраических уравнений
Использование задачи Коши.
Для решения так поставленной обратной тепловой задачи используем решения известной из математического анализа задачи Коши.
Зададим в пространстве переменных
С каждой точкой
в окрестности поверхности Г, такое, чтобы оно удовлетворяло следующим условиям Коши:
где
В результате простых математических выкладок, получим искомое решение задачи (1), (2), записанное в виде:
Классическая теорема Коши - Ковалевской говорит о существовании решения (3), об аналитичности этого решения и его единственности в классе аналитических функций .
При заданных
Получили типичную некорректную задачу, для построения устойчивого решения которой необходимо построение регуляризирующих алгоритмов.
В такой интерпретации решения (3), где функции
В решении (3) сохраним конечное число слагаемых N. Пусть
Интегрируя эту систему, получим систему интегральных уравнений Вольтерра первого рода:
где k =1, 2, ... , N. Соотношения для теплового потока в (3) записывается аналогично. Предположим, что на поверхности X = 0 теплосъем отсутствует, то есть стенка теплоизолирована., тогда решение (3) с учетом обозначений (4) имеет вид:
Граничные условия при X = 1 восстанавливаются соотношением (6), в котором функции
правая часть этого соотношения задается приближенно, то есть
В общем случае задача (7) является некорректно поставленной. Алгоритм, основанный на минимизации функционала А.Н.Тихонова является в настоящее время наиболее распространенным и эффективным регуляризующим алгоритмом для ее решения задачи (7). Этот алгоритм обладает устойчивостью к малым возмущениям правой части. Объясним, как преобразуется правая часть уравнения (7) при решении.
Функция
где ,
По так называемому принципу невязки выбрали следующий параметр регуляризации
Возможность представления системы пластин теплового отношения (рис.1) в виде пластины из теплозащитного покрытия и оболочки, которую можно рассматривать как тепловую емкость, следует из анализа теплофизических и геометрических характеристик конструкции камеры сгорания. Это предположение дает возможность воспользоваться решением задачи Коши (3) для построения решения обратной тепловой задачи для заданного узла. В представленной на Рис.1 системе координат, поверхность при X = 0 будем считать теплоизолированной:
Если система пластин в начальный момент времени прогрета равномерно и, тогда начальные условия для функции
При сделанных выше предположениях условия Коши (12) для этой задачи имеют вид
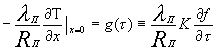 , (13)
, (13)
Подставляя значение
где
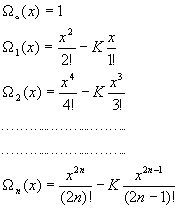
Таким образом, решение этой задачи имеет вид
где
(7) - (9).
Искомые величины
Погрешности решений обратных задач теплопроводности.
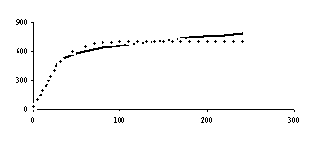
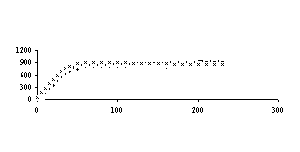
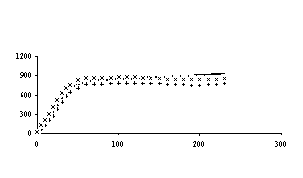
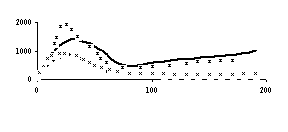
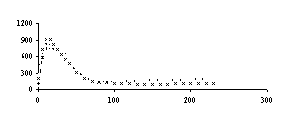
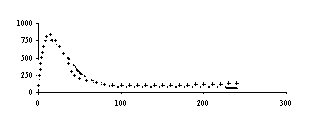
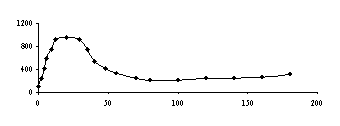
На рисунках 4, 5, 6 ,7 и 8 соответственно представлены зависимости температуры поверхности и экспериментальной температуры от времени, а также теплового потока и коэффициента теплоотдачи. Измерения температуры, необходимые для обратной тепловой задачи, в реальных условиях являются случайными величинами из-за дефектов производства, технологии изготовления, загрязнения поверхности, погрешности измерения и обработки экспериментальной информации. С помощью метода статистических испытаний Монте – Карло можно подсчитать влияние погрешностей исходной информации на решение обратной задачи теплопроводности. Метод статистических испытаний Монте - Карло. Анализ результата статистического моделирования решения обратной задачи позволяет установить коридор ошибок искомых граничных условий. Метод статистических испытаний Монте –Карло, который заключается в статистическом моделировании аналитических решений ОЗТ с учетом случайного характера исходных данных, является одним из методов решения обратной тепловой задачи. В данном методе этого необходим источник случайных чисел, потому что в методе Монте-Карло основным является случайная выборка исходных данных. Для исходных данных введём обозначение
где
где
При возмущении по нормальному закону распределения плотностей вероятностей используем правило "трех сигм". Метод Монте – Карло даёт возможность оценить влияние на решение ОЗТ погрешности исходной информации (геометрические размеры, место установки температурного датчика, теплофизические характеристики, измерения и обработки экспериментальной температуры внутренних точек тела). Кроме того, процедура Монте – Карло позволяет рассматривать влияние каждой входной величины на решение ОЗТ. Так называемый коридор ошибок восстановленного решения можно определить по результатам статистической обработки полученных реализации.
Найденные таким путем статистические характеристики решения ОЗТ можно использовать для того, чтобы направить инженерные усилия на уменьшение именно тех случайных вариаций, которые наиболее сильно сказываются на решении ОЗТ. Погрешность в задании экспериментальной температуры до 5%,как показали приведённые расчеты для однослойной пластины, используемой выше, вызывает максимальные отклонения температуры поверхности до 10% на временном интервале 0 - 55 сек, а на остальном временном участке до 5%. 20% и 10% соответственно составляют максимальные отклонения теплового потока на тех же временных интервалах. Аналогичные расчеты, проведённые уже для двухслойной пластины показали, что погрешность в задании экспериментальной температуры до 5% вызывает максимальные отклонения температуры до 10% на временном интервале 0 - 50 сек, а на остальном временном участке до 5%. Максимальные отклонения теплового потока на тех же временных интервалах составляют соответственно 20% и 10%.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
С. 37 – 41.
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
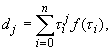
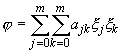 неотрицательна для любых значений переменных
неотрицательна для любых значений переменных
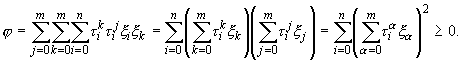
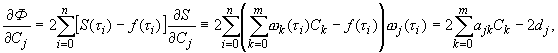
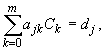
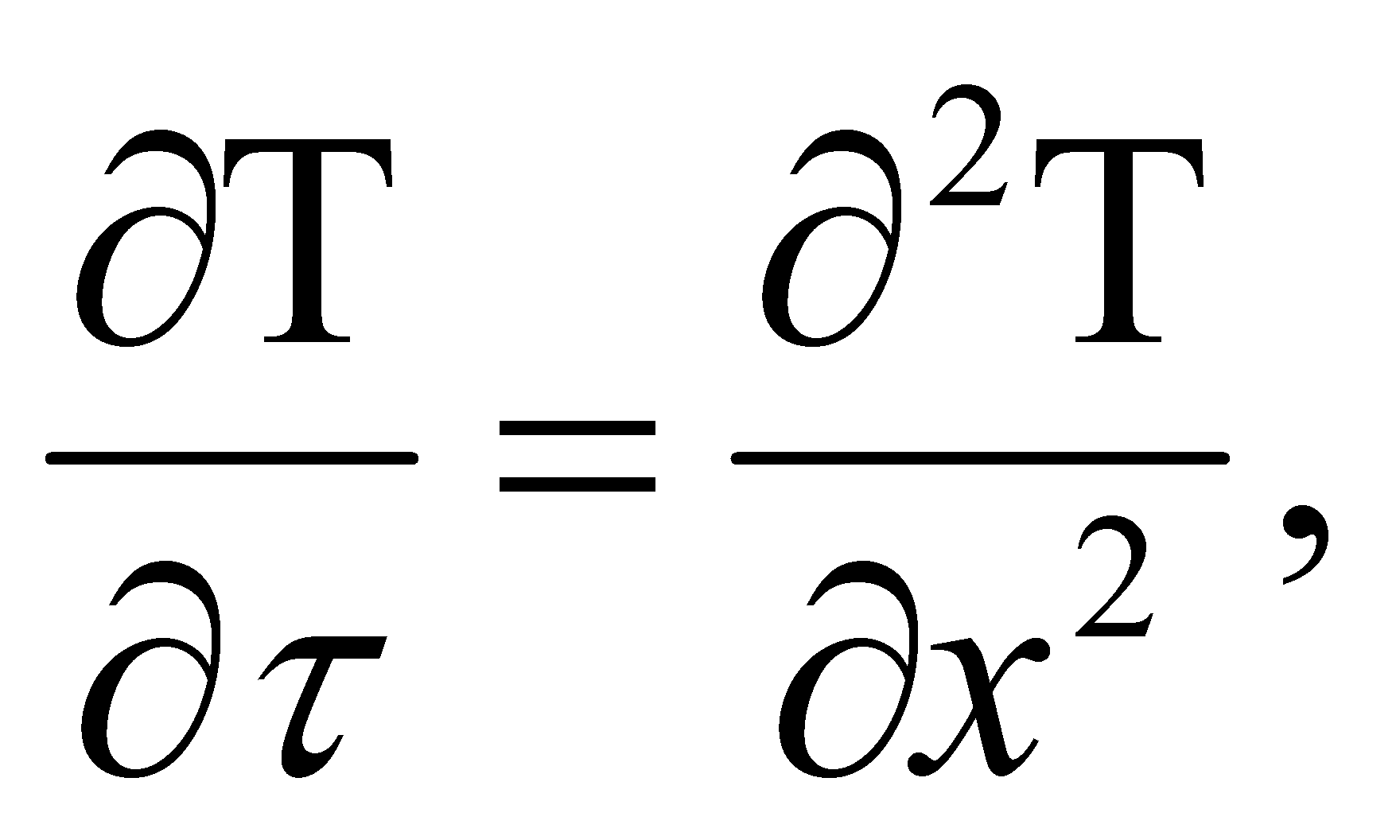 Решение уравнения
Решение уравнения
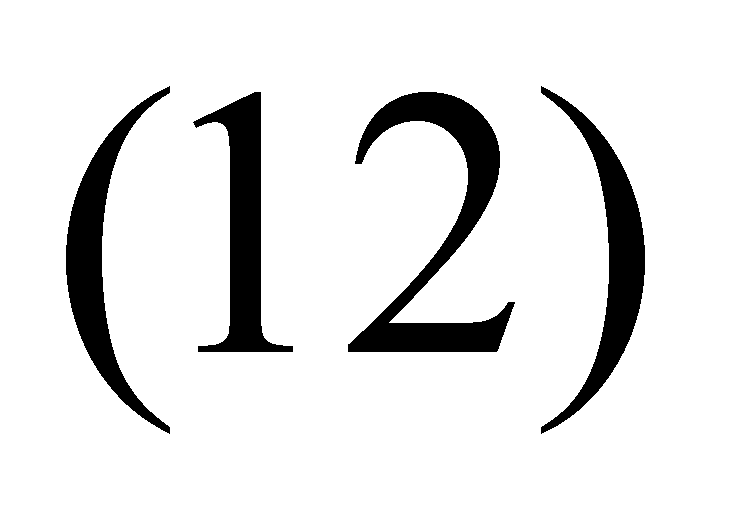
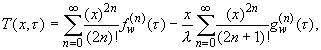 (3)
(3)
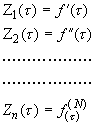 (4)
(4)
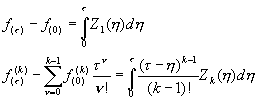 , (5)
, (5)
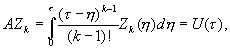 (7)
(7)
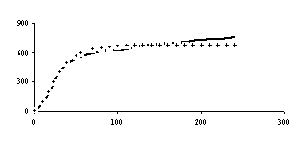
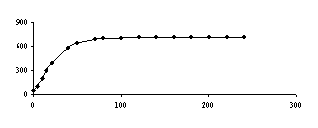
 Главная
Главная