Конспекты лекций по математической логике
1.1 Различные подходы к определению алгоритма: 1 0 . Неформальное понятие алгоритма (последовательность инструкций для выполнения действия). 2 0 . Машина с неограниченными регистрами (МНР). 3 0 Машина Тьюринга – Поста (МТ-П). 4 0 Нормальные алгоритмы Маркова (НАМ). 1.1.1 Машина с неограниченными регистрами (МНР).
Допустимые команды: Z(n) - обнуление регистра R n . S(n) - увеличение числа в регистре R n на 1. T(m,n) - копирует содержимое R m в регистор R n . I(p,q,n) - если содержимое R p = R q то выполняется команда с номером n , если нет следующая. Программа для МНР должна быть последовательностью команд Z, S, T, I с определенным порядком, выполняемые последовательно.
Тезис Черча (Churcha) : Первое и второе определение алгоритма эквивалентны между собой. Любой неформальный алгоритм может быть представлен в программе для МНР.
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие элементы алфавита:
Слово в данном алфавите - любая конечная упорядоченная последовательность букв данного алфавита, притом длина слова это количество букв в нем (у пустого слова длина 0). Допустимые команды:
1.1.3 Нормальные алгоритмы Маркова.
Тип машины перерабатывающий слова, в которой существует некий алфавит
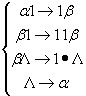
Допустимые команды: (Для машин этого типа важна последовательность команд.)
1.1.4 Реализация функции натурального переменного.
притом
притом
(
1.2 Эквивалентность трех подходов к понятию алгоритм. 1.2.1 Теорема об эквивалентности понятия вычислимой функции.
)
Использование НАМ:
Пусть
МТ-П: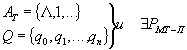 
НАМ:
Команда МТП:
Команда МТП:
2. Булевы функции. 2.1 Основные определения 2.1.1 Декартово произведение
Пример
:
2.1.2 Декартова степень произвольного множества.
Опр
:
2.1.3 Определение булевой функции от n переменных.
Любое отображение
2.1.4 Примеры булевой функции.
2.1.5 Основные булевы тождества.
2.2 Дизъюнктивные нормальные формы. 2.2.1 Основные определения.
Рассмотрим слово:
Экспоненциальные обозначения:
S – длина элемента конъюнкции. ДНФ – дизъюнкция нескольких различных элементарных конъюнкций.
Любая булева функция может быть представлена как ДНФ 2.2.2 Теорема о совершенной ДНФ.
Любая булева функция
Опр
: Носитель булевой функции
Лемма
:
а)
б)
Доказательство:
Следовательно
2.2.3 Некоторые другие виды ДНФ.
Опр:
Опр:
(Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не верно.)
Опр:
К-мерной гранью
называется такое подмножество
Опр: Предположим дана функция
Опр: Максимальная грань – это такая грань, которая не содержится ни в какой грани более высокой размерности. Предложение: Любую отмеченную грань можно вложить в максимальную грань.
Предложение:
(Носитель любой функции можно разложить в объединение нескольких граней разной размерностей)
Предложение: Носитель любой функции разлагается в объединение всех своих максимальных граней.
Опр: Элементарная конъюнкция называется минимальной , если её носитель является максимальной гранью. Следовательно всякая булева функция разлагается в дизъюнкцию всех своих элементарных конъюнкций. Опр: Сокращенная ДНФ – разложение данной булевой функции в соответствующие ДНФ, которые соответствуют объединению её максимальных граней. Теор: Минимальная ДНФ может быть получена из сокращенной отбрасыванием некоторого количества слагаемых, возможно пустого. 3 Логические Исчисления. 3.1 Исчисления высказывания (ИВ). 3.1.1 Определения.
Опр: V – словом в алфавите А , называется любая конечная упорядоченная последовательность его букв.
Опр:
Формативная последовательность слов
– конечная последовательность слов и высказываний
Опр: F – формулой ИВ , называется любое слово, входящее в какую-нибудь формативную последовательность.
Пример:
Опр:
Аксиомы
– специально выделенное подмножество формул.
Reg – правила вывода ИВ (некоторые правила преобразования первого слова в другое).
a
– символ переменной
Отображение
Пример:
Правило modus ponens
:
3.1.2 Формальный вывод.(простейшая модель доказательства теоремы) Опр: Последовательность формул ИВ, называется формальным выводом, если каждая формула этой последовательности имеет следующий вид:
Опр: Выводимый формулой (теоремой) ИВ называется любая формула входящая в какой-нибудь формальный вывод.
Пример:
Правило одновременной подстановки.
Замечание
: Если формула
Возьмем формативную последовательность вывода
(Если выводима
Теор: Если выводимая формула
Выберем
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез
Лемма:
Напишем список:
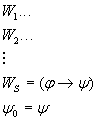
Лемма
:
Док:
3.1.4 Теорема Дедукции. Если из
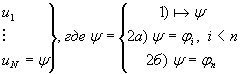
2б)
Базис индукции: N=1
Пример:
3.2 Критерий выводимости в ИВ. 3.2.1 Формулировка теоремы.
при любой интерпретации алфавита (символов переменных)
3.2.2 Понятие интерпретации.
символ переменной
- проекция на
.
- только символ
переменных, т.к. это заглавное слово формативной последо- вательности вида:
Где:
3.2.3 Доказательство теоремы.
вывод
3.3 Непротиворечивость ИВ. 3.3.1 Определение.
ИВ
противоречиво
.
ИВ непротиворечиво , если оно не является противоречивым.
Теорема : ИВ является непротиворечивым исчислением по отношению к любому из трех определений.
Док-во
: (1) Если
(2) Если любая формула выводима, то выводима и А , что соответствует пункту 1.
(3) Пусть
3.4 Формальные исчисления. Алфавит – конечное или счетное множество символов, возможно, разбитых на группы. Алфавит должен быть упорядоченным множеством. Слово – конечная упорядоченная последовательность символов алфавита, в т.ч. пустое слово. V – множество всех слов.
Вычислимая функция от нескольких натуральных переменных
( f – может быть не всюду определенной )
f – называется
вычислимой
, если
Множество
М
- разрешимо
М
– перечислимо
Множество всех формул F – некоторое разрешимое подмножество V .
Т
– счетное множество, если
- алеф-нуль)
Если
то L – ансамбль . V – ансамбль (слова лексикографически упорядочены и занумерованы)
Определение
: В произвольном формальном исчислении:
Правило вывода:
разрешимо. Для ИВ
N
=2.
Пример :
(пустое слово) ,
3 – не является формальным выводом.
4 Предикаты и кванторы. 4.1 Определение предиката.
Пусть А – множество объектов произвольной природы ( предметная область предиката ).
- характеристическая функция от x на множестве А - совпадает с предикатами
4.2 Понятие квантора.
n – свободная переменная
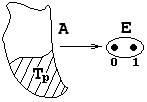
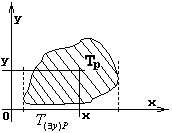
4.3 Геометрическая интерпретация навешивания кванторов.
Пронесение отрицания через кванторы
Геометрическое 'доказательство':
целиком лежит в
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
Имеется некое устройство, в котором счетное число ячеек памяти (регистров), в которых хранятся целые числа.
, где
- пустой символ (пустое слово), который может принадлежать и не принадлежать
А
. Также существует управляющая головка (устройство) (УУ)/(УГ), которая в начальный момент расположена в определенном месте, в состоянии
. Также существуют внутренние состояния машины:
,где
.
(остановка программы).
, для которого W - множество всех слов.
но мы допускаем не всюду определенную функцию.
, если
f
не определена, то и программа не должна ничего выдавать.
, если
f
не определена, то и программа не должна ничего выдавать.
, а числа представляются в виде
,например
.)
которая вычисляется на МТ-П, вычислим её на НАМ.
преобразуется по правилам:
- множество всевозможных упорядоченных наборов длины n , элементов множества А.
- называется булевой функцией от n переменных, притом множество
- элемент конъюнкции.
тождественно не равная 0 может быть разложена в ДНФ следующего вида:
.
возьмем набор
, будем доказывать, что
.
. Возьмем
он попадает в число суммируемых наборов и по нему будет проводиться сумирование.
. Возьмем другой набор из
- называется
минимальной ДНФ
, если она имеет
- наименьшую возможную длину из всех ДНФ данной функции.
, которая является носителем некоторой элементарной конъюнкции длины: n-k.
и есть
. Грань называется
отмеченной
, если она целиком содержится в носителе
Т
.
, если они имеют формат вида:
- произвольное слово ИВ (формула)
действует так, что на место каждого вхождения символа
а
, пишется слово
- выводимая формула ИВ.
выводима, то выводима и
, получившаяся последовательность является формальным выводом.
, то выводима
)
(
- различные символы переменных) выводима
- символы переменных которые различны между собой и не входят не в одну из формул
, сделаем подстановку
и последовательно применим
и в новом слове делаем последовательную подстановку:
, где
- является формальным выводом.
(формулы), называется такая последовательность слов
, каждая из которых удовлетворяет условию:
если формулу
.
;
: то тогда
, где
по правилу m.p.
- уже выводили
, ч.т.д.
(только что доказано), осуществим переход по индукции:
по индукции
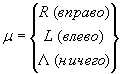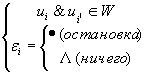
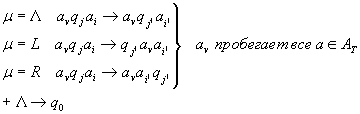
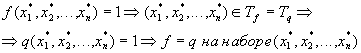
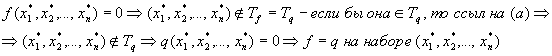
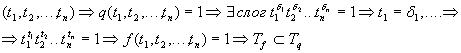
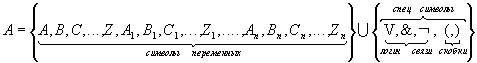
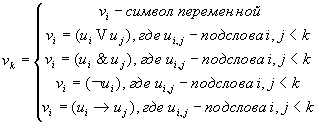
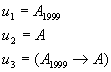
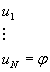
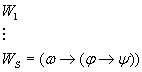
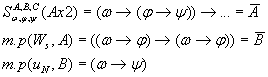
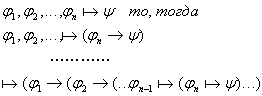
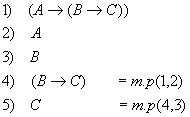по теореме дедукции
переменную поставим в соответствие.
формальный
.
, то соответствующая ей булева функция будет тождественно равна 1.
- булева функция
- противоречие.
такая машина Тьюринга, которая её вычисляет.
называется перечислимым, если
М
и
N
\
M
перечислимы.
его биективное отображение на
V
.
и зафиксировано биективное и вычислимое отображение
(вычис.),
- множество всех аксиом – разрешимое подмножество множества всех формул.
1 и 2 – формальные выводы.
- высказывание, содержащее переменную.
- ортогональная проекция на ось x
ч.т.д.
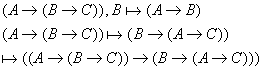
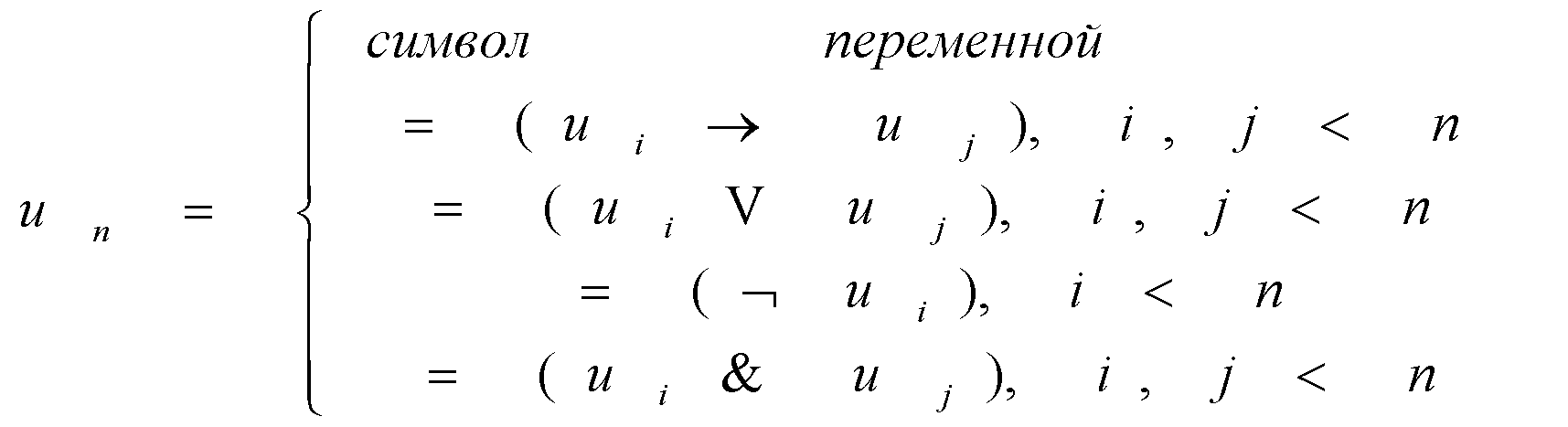
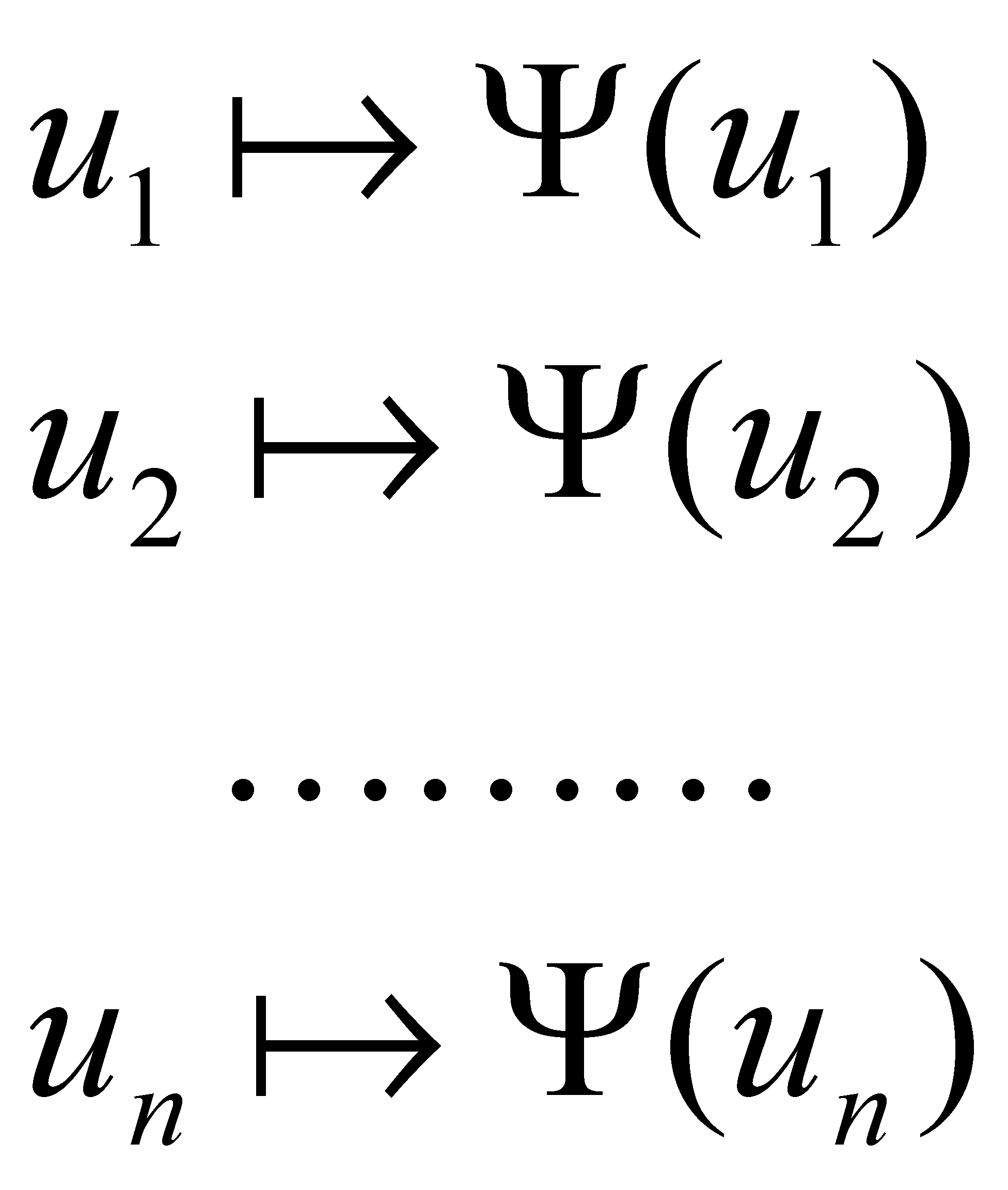
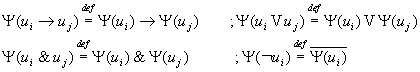
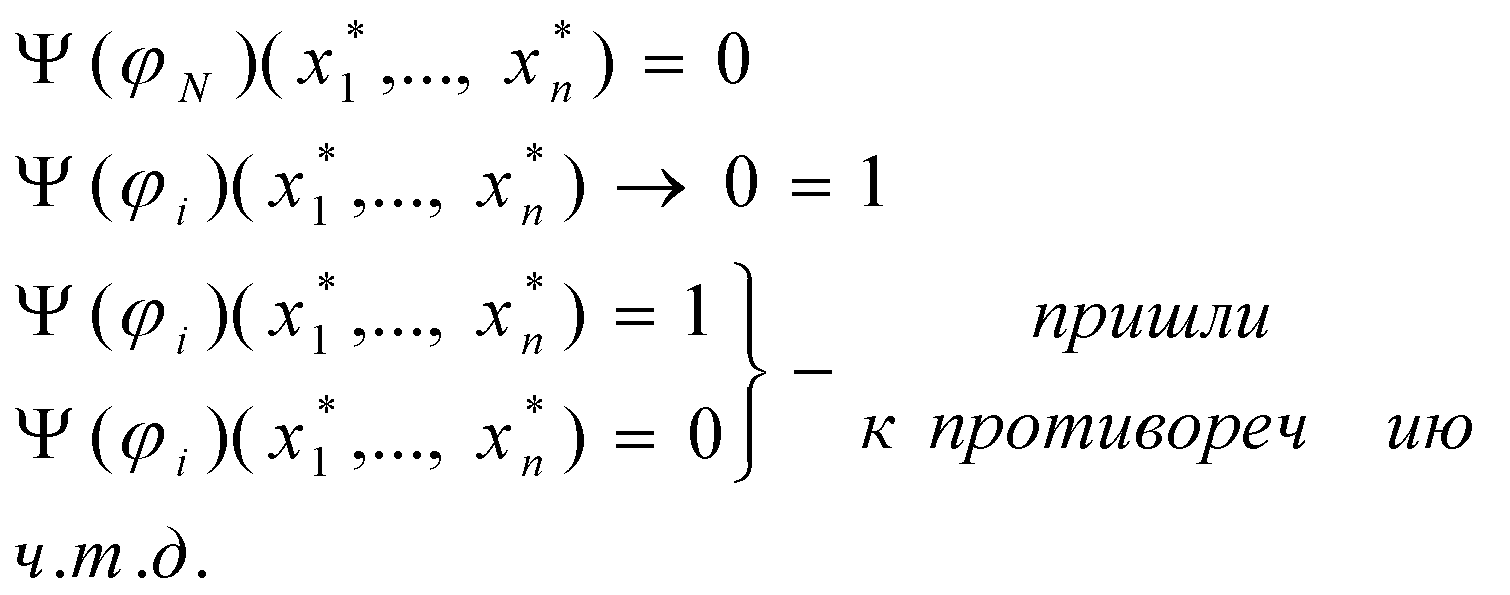
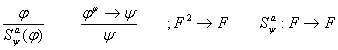
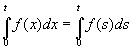
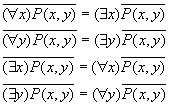
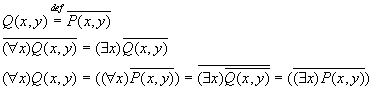
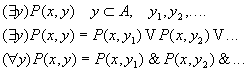
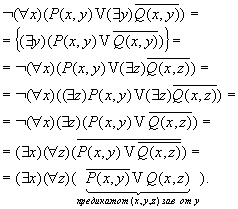
Главная