Образцы исследования элементарных функций, содержащих обратные тригонометрические функции
Примеры Примеры: в нижеследующих примерах приведены образцы исследования элементарных функций, заданных формулами, содержащими обратные тригонометрические функции. Пример №1. Исследовать функции arcsin(1/x) и arccos(1/y) и построить их графики. Решение: Рассмотрим 1-ю функцию
y = arcsin(1/x)
Д(f): | 1/x | ≤ 1 ,
| x | ≥ 1 , ( - ∞ ; -1 ] U [ 1; + ∞ )
Функция нечетная
( f(x) убывает на пр. [0;1] , f(y) убывает на пр. [0; π/2 ] )
Заметим, что функция y=arccosec(x) определяется из условий cosec(y)=x и y є [- π/2 ; π/2 ], но из условия cosec(y)=x следует sin(y)=1/x, откуда y=arcsin(1/x). Итак, arccos(1/x)=arcsec(x)
Д(f): ( - ∞ ; -1 ] U [ 1; + ∞ )
Пример №2. Исследовать функцию y=arccos(x 2 ). Решение:
Д(f): [-1;1] Четная f(x) убывает на пр. [0;1]
f(x) возрастает на пр. [-1;0]
Пример №3. Исследовать функцию y=arccos 2 (x). Решение: Пусть z = arccos(x), тогда y = z 2 f(z) убывает на пр. [-1;1] от π до 0.
Пример №4. Исследовать функцию y=arctg(1/(x 2 -1)) Решение: Д(f): ( - ∞ ; -1 ) U ( -1; 1 ) U ( 1; +∞ ) Т.к. функция четная, то достаточно исследовать функцию на двух промежутках: [ 0 ; 1 ) и ( 1 ; +∞ )
Тригонометрические операции над аркфункциями Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна через другую, поэтому в результате выполнения какой-либо тригонометрической операции над любой из аркфункций получается алгебраическое выражение. В силу определения аркфункций: sin(arcsin(x)) = x , cos(arccos(x)) = x (справедливо только для x є [-1;1] ) tg(arctg(x)) = x , ctg(arcctg(x)) = x (справедливо при любых x ) Графическое различие между функциями, заданными формулами:
y=x и y=sin(arcsin(x))
Сводка формул, получающихся в результате выполнения простейших тригонометрических операций над аркфункциями.
Справедливость всех этих формул может быть установлена при помощи рассуждений, приведенных ниже:
Перед радикалом
Значит, имеем
Ниже приведены образцы выполнения различных преобразований посредством выведения формул.
Пример №1. Преобразовать выражение
Решение: Применяем формулу
Пример №2. Подобным же образом устанавливается справедливость тождеств:
Пример №3. Пользуясь
Пример №4. Аналогично можно доказать следующие тождества:
Пример №5. Положив в формулах
Пример №6. Преобразуем
Положив в формуле
Получим:
Перед радикалами взят знак “+”, т.к. дуга
Соотношения между аркфункциями Соотношения первого рода – соотношения между аркфункциями, вытекающими из зависимости между тригонометрическими функциями дополнительных дуг. Теорема. При всех допустимых х имеют место тождества:
Соотношения второго рода – соотношения между аркфункциями, вытекающие из соотношений между значениями тригонометрических функций от одного и того же аргумента. Посредством соотношений 2-го рода производятся преобразования одной аркфункции в другую (но от различных аргументов). Случай №1. Значения двух данных аркфункций заключены в одной и той же полуокружности. Пусть, например, рассматривается дуга α, заключенная в интервале (-π /2; π/2).
Данная дуга может быть представлена как в виде арксинуса, так и в виде арктангенса. В самом деле, дуга
Аналогично можно дугу α представить в виде арктангенса:
А если бы дуга α была заключена в интервале ( 0 ; π ), то она могла бы быть представлена как в виде арккосинуса, так и в виде арккотангенса:
Так, например:
Аналогично:
Формулы преобразования одних аркфункций в другие, значения которых содержаться в одной и той же полуокружности (правой или верхней).
Пусть
Дуга
Дуга
Следовательно,
(в интервале ( -1 : 1 )
Т.к.
в интервале
Случай №2. Рассмотрим две аркфункции, значения которых выбираются в различных промежутках (например, арксинус и арккосинус; арккосинус и арктангенс и т.п.). Если аргумент какой-либо аркфункции (т.е. значение тригонометрической функции) положителен, то соответственно аркфункция (дуга), заключенная в первой четверти, может быть представлена при помощи любой аркфункции; так, например,
Поэтому каждая из аркфункций от положительного аргумента может быть выражена посредством любой другой аркфункции. Значение какой-либо аркфункции от отрицательного аргумента принадлежит либо промежутку от -π/2 до 0, либо промежутку от π/2 до π и не может быть представлено в виде аркфункции, значение которой принадлежит другому (из этих двух) промежутку.
Так, например, дуга
Формулы преобразования одних аркфункций в другие, значения которых выбираются в различных полуокружностях.
Пусть
При
имеем:
так как аргумент арккосинуса есть арифметический корень
Расположение рассматриваемых дуг пояснено на рисунке:
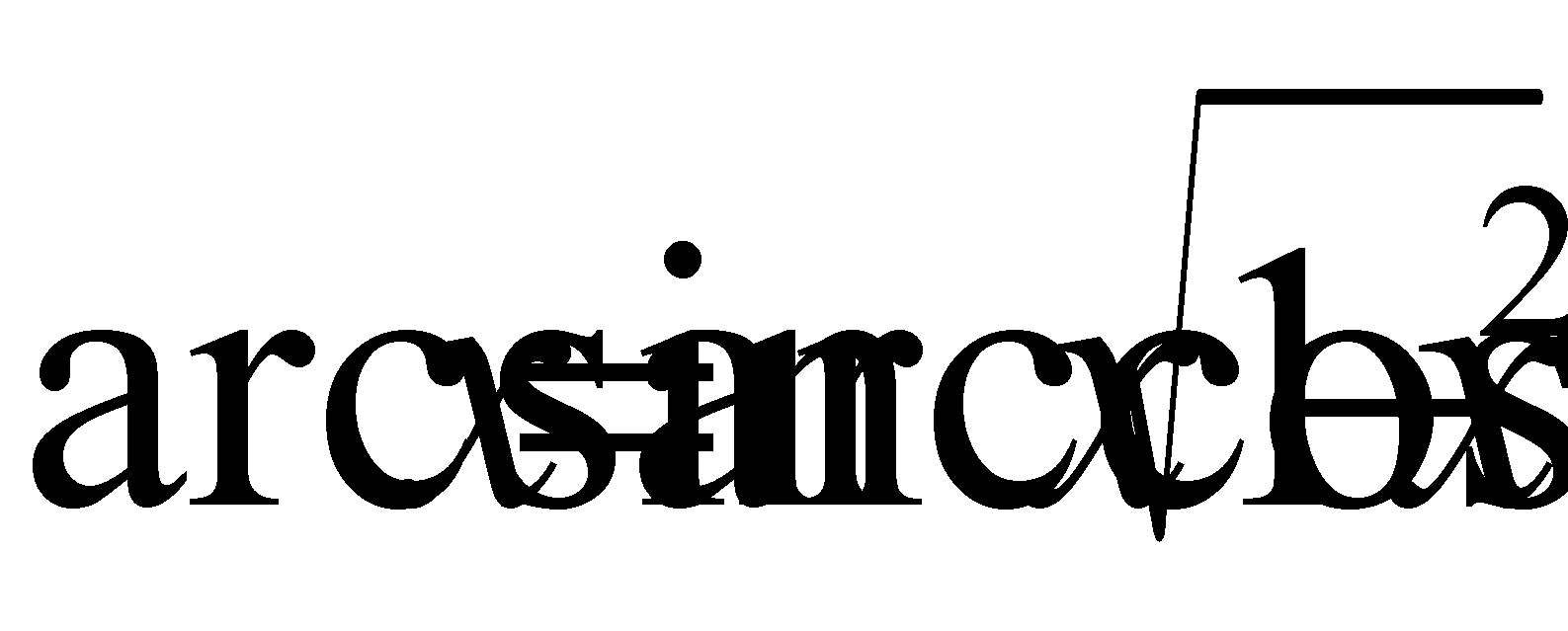
Х>0 X<0 При отрицательных значениях Х имеем Х<0, а при положительных X>0, и
Таким образом, имеем окончательно:
,
(4)
График функции 
Область определения есть сегмент [-1;1]; согласно равенству (4), закон соответствия можно выразить следующим образом:
, если
, то
Таким образом:
(5)
имеем:
Если же х<0, то
Итак,
(6)
При
Итак,
, если
(7)
, если х>0
(8)
При x>0 равенство (8) легко установить; если же x<0, то
, если
(9)
, если 0<x
(10)
, если x>0
(11)
Примеры:
Пример №1. Исследовать функцию
Решение. Эта функция определена для всех значений х, за исключением значения х=0 (при х=0) второе слагаемое теряет смысл). Воспользовавшись формулой (8) получим:
y= 0 , если x>0 -π , если x<0
данной функции
Пример №2. Исследовать функцию
Решение: Первое слагаемое определено для значений
Т.к.
откуда:
Пример №3. Исследовать функцию
Решение: Выражения, стоящие под знаками аркфункций не превосходят по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (4).
Приняв во внимание равенство
, если
получим: y = 0 , если 
Выполнение обратных тригонометрических операций над тригонометрическими функциями. При преобразовании выражений вида
следует принимать во внимание в какой четверти находится аргумент х и в каком промежутке находится значение данной аркфункции. Рассмотрим, например, первое из данных выражений:
Согласно определению арксинуса, y – есть дуга правой полуокружности (замкнутая), синус которой равен sin x ;
Областью определения функции
Так, например, при х=π/6 имеем:
но при х=5π/6
В силу периодичности синуса функция arcsin x также является периодической с периодом 2π, поэтому достаточно исследовать ее на сегменте [- π /2; 3 π /2] величиной 2π. Если значение х принадлежит сегменту [- π /2; π /2] то y=x, на этом сегменте график функции совпадает с биссектрисой координатного угла. Если значение х принадлежит сегменту [ π /2; 3 π /2], то в этом случае дуга π-х принадлежит сегменту [- π /2; π /2]; и, так как
в этом промежутке график функции совпадает с прямой линией y= π-υ . Если значение х принадлежит сегменту [3 π /2; 5 π /2], то, пользуясь периодичностью или путем непосредственной проверки, получим: y=х-2 π Если значение х принадлежит сегменту [-3 π /2; - π /2], то y=- π-υ Если значение х принадлежит сегменту [-5 π /2; -3 π /2], то y=х+2 π
Вообще, если
y=х-2 π k
и если
y=( π- х)+2 π k
График функции
Рассмотрим функцию
Согласно определению арккосинуса, имеем:
cos
y =
cos
x
, где
Областью определения данной функции является множество всех действительных чисел; функция периодическая, с периодом, равным 2π. Если значение Х принадлежит сегменту [0;
π
], то y = x. Если х принадлежит сегменту [
π
; 2
π
], то дуга 2π-х принадлежит сегменту [0;
π
] и
Следовательно, на сегменте [ π ; 2 π ] имеем y = 2 π - x Если х принадлежит сегменту [2 π ; 3 π ], то y = x - 2 π Если х принадлежит сегменту [3 π ; 4 π ], то y = 4 π – x
Вообще, если
Если же
Графиком функции
Формулы сложения Формулы сложения дают выражения для суммы или разности двух (или нескольких) аркфункций через какую-либо данную аркфункцию. Пусть дана сумма аркфункций; над этой суммой можно выполнить любую тригонометрическую операцию. (....) В соответствии с этим дуга-функция может быть выражена посредством любой данной аркфункции. Однако в различных случаях (при одних и тех же аркфункциях) могут получаться различные формулы, в зависимости от промежутка, в котором берется значение рассматриваемой аркфункции. Сказанное пояснено ниже на числовых примерах. Примеры. Пример №1. Преобразовать в арксинус сумму
Решение: эта сумма является суммой двух дуг α и β, где
В данном случае
Вычислив синус дуги γ, получим:
Т.к. сумма γ заключена на сегменте [- π /2; π /2], то
Пример №2. Представить дугу γ, рассмотренную в предыдущем примере, в виде арктангенса. Имеем:
Откуда
Пример №3. Представить посредством арктангенса сумму
Решение: в данном случае (в отличие от предыдущего) дуга γ оканчивается во второй четверти, т.к.
В рассматриваемом примере
В данном случае
Пример №4. Представить дугу γ, рассмотренную в предыдущем примере, в виде арккосинуса. Решение: имеем
Обе дуги γ и
Так как суммы и разности любых аркфункций можно выражать при помощи произвольных аркфункций, то можно получать самые разнообразные формулы сложения. Однако все эти формулы выводятся при помощи однотипных рассуждений. Ниже в качестве примеров даются некоторые из формул сложения, по этим образцам можно получить аналогичные формулы в различных прочих случаях.
Формулы сложения аркфункций от положительных аргументов. Пусть α и β – две дуги, заключенные в промежутке от 0 до π/2 (первая четверть):
Сумма α
+ β η
аключена в верхней полуокружности
Разность α
– β η
аключена в правой полуокружности:
Следовательно, она может быть представлена в виде арксинуса, а также в виде арктангенса:
Так как значение всякой аркфункции от положительного аргумента заключено в интервале (0; π/2) то сумму двух аркфункций от положительных аргументов можно представить в виде арккосинуса, а также в виде арккотангенса, а разность двух аркфункций от положительных аргументов можно представить в виде арккосинуса, а также в виде арктангенса. Ниже приведены образцы соответствующих преобразований.
Имеем:
Откуда
Формулы сложения аркфункций от произвольных аргументов.
По определению арксинуса
,
откуда
Для дуги γ возможны следующие три случая:
Случай 1:
Если числа x и y разных знаков или хотя бы одно из них равно нулю, то имеет место случай 1.
В самом деле, при
откуда
При x > 0, y > 0 для дуги γ имеет место одна из следующих двух систем неравенств:
а)
Необходимым и достаточным признаком, позволяющим отличить один от другого случаи а) и б), является выполнение неравенства:
в случае б)
В самом деле, взаимно исключающие друг друга соотношения а) и б) влекут за собой взаимно исключающие следствия
Вычислив
При
x
> 0,
y
> 0 наличие случая 1 означает выполнения неравенства а) т.е.
Откуда
Наличие случая 1 при x < 0, y < 0 означает выполнение неравенств
но тогда для положительных аргументов –x и –y имеет место случай 1, а потому
Случай 2.
В этом случае
x
> 0,
y
> 0, т.е. выполняется неравенство б); из условия
Случай 3.
Этот случай имеет место при
x
< 0,
y
< 0, и
Изменив знаки на противоположные придем к предыдущему случаю:
откуда
Дуги γ и
в случае 2
Итак, имеем окончательно:
,
или
Пример:
2. Заменив в (1) x на –x получим:
,
или
3. Выразить сумму
имеем
Возможны следующие два случая.
Случай 1:
Приняв во внимание, что обе дуги
и следовательно,
Случай 2:
откуда при помощи рассуждений, аналогичных предыдущим, получим
Из равенства
имеют одинаковый косинус.
В случае 1
,
4. Аналогично
,
пример:
5.
;
xy
< 1
;
x
> 1,
xy
> 1
(5)
При xy =1 не имеет смысла
6.
;
x
> 0,
xy
< -1
(6)
7.
;
8.
;
(8)
9.
;
10.
, если
(12)
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
следует взять знак “+”, т.к. дуга
принадлежит правой полуокружности (замкнутой)
, на которой косинус неотрицательный.
следует:
, имеем:
,
принадлежит I четверти, а потому левая часть неотрицательная.
имеет синус, равный sin
α θ
заключена, так же как и α, в интервале (-π
/2; π/2), ρ
ледовательно
через арктангенс.
, тогда
, по определению арктангенса, имеет тангенс, равный
и расположена в интервале (-π
/2; π/2).
имеет тот же тангенс и расположена в том же интервале (-π
/2; π/2).
(1)
через арксинус.
, то
(2)
следует тождество
(3)
не может быть значением арксинуса. В этом случае
, если
, то
. Дуга имеет косинус, равный
, а поэтому
это равенство выполняться не может. В самом деле, в этом случае
, т.е. число неотрицательное.
, если
, если
имеем:
, если
, если
, то
имеем:
, если
,если x<0
, если
, если х<0
, если x<0
, второе – для тех же значений аргумента. Преобразим первое слагаемое по формуле (4).
, то получаем
, если
, если
служит интервал
, так как при всех действительных значениях х значение промежуточного аргумента
содержится на сегменте
. При произвольном действительном х значение y (в общем случае) отлично от значения х.
, то
, то
, поэтому:
, то y = x - 2
π
k
, то
y = -x + π
k
является ломаная линия
(т.к.
, а следовательно,
), а также
, поэтому
.
, а
. Вычисляем
, так как дуги γ и
заключены в различных интервалах,
расположены в верхней полуокружности и имеют одинаковый косинус, следовательно, эти дуги равны:
, следовательно, ее можно представить в виде аркфункции, значение которой выбирается в том же интервале, т.е. в виде арккосинуса, а также в виде арккотангенса:
, где
и
, имеем:
, и
,
б)
(соответственно), а потому эти следствия служат необходимыми и достаточными признаками наличия данных соотношений.
, получим:
или
и, следовательно,
;
или
получим
имеют одинаковый синус, но (по определению арксинуса)
, следовательно в случае 1
;
и в случае 3
.
;
x
> 0,
y
> 0, и
(1)
;
x
< 0,
y
< 0, и
;
;
x
> 0,
y
> 0, и
;
x
< 0,
y
< 0, и
через арккосинус
, то
и
расположены в промежутке
[0;π]
и что в этом промежутке косинус убывает, получим
, откуда
. Если
, то
. Из сопоставления результатов следует, что случай 1 имеет место, если
, а случай 2, если
следует, что дуги
, следовательно,
,
(3)
;
x
< 0,
xy
> 1
;
xy
> -1
;
x
< 0,
xy
< -1
;
(7)
;
;
;
x
> 1
(9)
;
x
< -1
(10)
(11)
, если
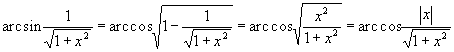
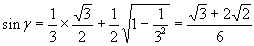
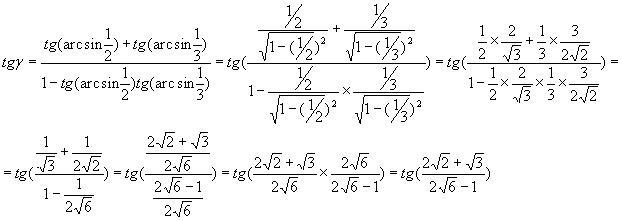
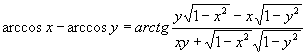
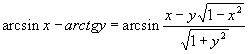
Главная