ÌÎÑÊÎÂÑÊÈÉ ÝÍÅÐÃÅÒÈ×ÅÑÊÈÉ ÈÍÑÒÈÒÓÒ (òåõíè÷åñêèé óíèâåðñèòåò)
ÔÀÊÓËÜÒÅÒ ÝËÅÊÒÐÎÍ Н ÎÉ ÒÅÕÍÈÊÈ
ÐÅÔÅÐÀÒ ÏÎ ÒÅÌÅ
Ê ÈÍÅÒÈ×ÅÑÊÎÅ ÓÐÀÂÍÅÍÈÅ Á ÎËÜÖÌÀÍÀ.
ÂÛÏÎËÍÈË: Êîðêèí Ñ.Â. ÃÐÓÏÏÀ: ЭТ-9-00
ÏÐÅÏÎÄÀÂÀÒÅËÜ Øåðêóíîâ Þ.Á.
Âòîðàÿ ïîëîâèíà ðàáîòû íàáèòà äîñòàòî÷íî ñëîæíîé ìàòåìàòèêîé . Àâòîð ( KorkinSV@mpei.ru , korkin_s_v@chat.ru)íå ñ÷èòàåò ýòîò êóðñîâîé èäåàëüíûì, îí ìîæåò ñëóæèòü ëèøü îòïðàâíîé òî÷êîé äëÿ íàïèñàíèÿ áîëåå ñîâåðøåííîé (è ïîíÿòíîé) ðàáîòû. Òåêñò íå ÿâëÿåòñÿ êîïèåé êíèãè. Âñïîìîãàòåëüíóþ ëèòåðàòóðó ñì. â êîíöå. Êóðñîâîé ïðèíÿò ñ îòìåòêîé ÎÒË. (Îêîí÷àòåëüíûé âàðèàíò ðàáîòû íåìíîæêî çàòåðÿëñÿ. Ïðåäëàãàþ âîñïîëüçîâàòüñÿ ïðåäïîñëåäíåé “âåðñèåé”).
2002 ãîä. Ñîäåðæàíèå: Ââåäåíèå……………………………………………………………………………… 3 Óñëîâíûå îáîçíà÷åíèÿ………………………………………………………………. 4 § 1 Ôóíêöèÿ ðàñïðåäåëåíèÿ. § 2 Ñòîëêíîâåíèå ÷àñòèö. § 3 Îïðåäåëåíèå âèäà èíòåãðàëà ñòîëêíîâåíèé è óðàâíåíèÿ Áîëüöìàíà. § 4. Êèíåòè÷åñêîå óðàâíåíèå äëÿ ñëàáî íåîäíîðîäíîãî ãàçà. Òåïëîïðîâîäíîñòü ãàçà.
Некоторые условные обозначения: n - концентрация частиц; d - среднее расстояние между частицами; V - некоторый объём системы; P - вероятность некоторого события; f - функция распределения;
Ââåäåíèå. Ðàçäåëû ôèçèêè òåðìîäèíàìèêà, ñòàòèñòè÷åñêàÿ ôèçèêà è ôèçè÷åñêàÿ êèíåòèêà çàíèìàþòñÿ èçó÷åíèåì ôèçè÷åñêèõ ïðîöåññîâ, ïðîèñõîäÿùèõ â ìàêðîñêîïè÷åñêèõ ñèñòåìàõ - òåëàõ, ñîñòîÿùèõ èç áîëüøîãî ÷èñëà ìèêðî÷àñòèö.  çàâèñèìîñòè îò âèäà ñèñòåìû òàêèìè ìèêðî÷àñòèöàìè ìîãóò ÿâëÿòüñÿ àòîìû, ìîëåêóëû, èîíû, ýëåêòðîíû, ôîòîíû èëè èíûå ÷àñòèöû. Íà ñåãîäíÿøíèé äåíü ñóùåñòâóþò äâà îñíîâíûõ ìåòîäà èññëåäîâàíèÿ ñîñòîÿíèé ìàêðîñêîïè÷åñêèõ ñèñòåì - òåðìîäèíàìè÷åñêèé, õàðàêòåðèçóþùèé ñîñòîÿíèå ñèñòåìû ÷åðåç ìàêðîñêîïè÷åñêèå ëåãêî èçìåðÿåìûå ïàðàìåòðû (íàïðèìåð, äàâëåíèå, îáú¸ì, òåìïåðàòóðà , количество молей или концентрация вещества ) è, ïî ñóòè, íå ó÷èòûâàþùèé àòîìíî-ìîëåêóëÿðíóþ ñòðóêòóðó âåùåñòâà, è ñòàòèñòè÷åñêèé ìåòîä, îñíîâàííûé íà àòîìíî-ìîëåêóëÿðíîé ìîäåëè ðàññìàòðèâàåìîé ñèñòåìû. Òåðìîäèíàìè÷åñêèé ìåòîä íå áóäåò çàòðàãèâàòüñÿ â äàííîé ðàáîòå. Ïî èçâåñòíûì çàêîíàì ïîâåäåíèÿ ÷àñòèö ñèñòåìû ñòàòèñòè÷åñêèé ìåòîä ïîçâîëÿåò óñòàíîâèòü çàêîíû ïîâåäåíèÿ âñåé ìàêðîñèñòåìû â öåëîì. Ñ öåëüþ óïðîùåíèÿ ðåøàåìîé çàäà÷è ïðè ñòàòèñòè÷åñêîì ïîäõîäå äåëàåòñÿ ðÿä ïðåäïîëîæåíèé (äîïóùåíèé) î ïîâåäåíèè ìèêðî÷àñòèö è, ñëåäîâàòåëüíî, ðåçóëüòàòû, ïîëó÷åííûå ñòàòìåòîäîì, ñïðàâåäëèâû ëèøü â ïðåäåëàõ ñäåëàííûõ äîïóùåíèé. Ñòàòèñòè÷åñêèé ìåòîä èñïîëüçóåò âåðîÿòíîñòíûé ïîäõîä ê ðåøåíèþ çàäà÷, äëÿ èñïîëüçîâàíèÿ ýòîãî ìåòîäà ñèñòåìà îáÿçàíà ñîäåðæàòü äîñòàòî÷íî áîëüøîå êîëè÷åñòâî ÷àñòèö. Îäíà èç çàäà÷, ðåøàåìàÿ ñòàòìåòîäîì, - âûâîä óðàâíåíèÿ ñîñòîÿíèÿ ìàêðîñêîïè÷åñêîé ñèñòåìû. Ñîñòîÿíèå ñèñòåìû ìîæåò áûòü íåèçìåííûì âî âðåìåíè (ðàâíîâåñíàÿ ñèñòåìà) ëèáî ìîæåò èçìåíÿòüñÿ ñ òå÷åíèåì âðåìåíè (íåðàâíîâåñíàÿ ñèñòåìà). Èçó÷åíèåì íåðàâíîâåñíûõ ñîñòîÿíèé ñèñòåì è ïðîöåññîâ, ïðîèñõîäÿùèõ â òàêèõ ñèñòåìàõ, çàíèìàåòñÿ ôèçè÷åñêàÿ êèíåòèêà. Óðàâíåíèå ñîñòîÿíèÿ ðàçâèâàþùåéñÿ âî âðåìåíè ñèñòåìû ïðåäñòàâëÿåò ñîáîé êèíåòè÷åñêîå óðàâíåíèå, ðåøåíèå êîòîðîãî îïðåäåëÿåò ñîñòîÿíèå ñèñòåìû â ëþáîé ìîìåíò âðåìåíè. Èíòåðåñ ê êèíåòè÷åñêèì óðàâíåíèÿì ñâÿçàí ñ âîçìîæíîñòüþ èõ ïðèìåíåíèÿ â ðàçëè÷íûõ îáëàñòÿõ ôèçèêè: â êèíåòè÷åñêîé òåîðèè ãàçà, â àñòðîôèçèêå, ôèçèêå ïëàçìû, ìåõàíèêå æèäêîñòåé. В данной работе рассматривается кинетическое уравнение, выведенное одним из основоположников статистической физики и физической кинетики австрийским физиком Людвигом Больцманом в 1872 году и носящее его имя.
§ 1 Функция распределения.
- частицы газа неразличимы (одинаковы); - частицы сталкиваются только попарно (пренебрегаем столкновением одновременно трех и более частиц); - непосредственно перед столкновением частицы движутся по одной прямой навстречу друг другу; - столкновение молекул есть прямой центральный упругий удар;
и . Обозначим через
Поступательное движение классической частицы описывается координатами
(рад/c)
За одну секунду молекула делает (т.е. приблизительно ) полных оборота. Скорость изменения угла поворота оси двухатомной молекулы велика и все возможные ориентации молекулы в плоскости вращения будут равновероятными. Тогда при рассмотрении реальных физических задач функцию распределения можно считать не зависящей от ориентации молекулы. Закон равнораспределения справедлив и для многоатомных молекул, а значит сделанное предположение о независимости функции распределения от ориентации молекул газа в пространстве можно считать справедливым для многоатомных газов. Колебательное движение атомов внутри молекулы практически всегда квантуется и состояние молекулы как квантовой системы должно определяться квантовыми параметрами. В обычных условиях (при не слишком высоких температурах) молекула газа находятся в невозбужденном состоянии, отвечающем основному (нулевому) колебательному уровню. Поэтому квантовыми эффектами в реальных газах при обычных условиях можно пренебречь. Следовательно, функция распределения классического идеального газа в неравновесном состоянии зависит не только от времени, но и от координат частиц .
является макроскопической величиной. Макроскопичность имеет место лишь в том случае, когда элементарный объём содержит достаточно большое число частиц ( только тогда изменение числа частиц в элементарном объёме мало в течение рассматриваемого процесса); при этом линейные размеры области, занимаемой газом, должны быть значительно больше среднего межмолекулярного расстояния.
§ 2 Столкновение частиц.
(1)
(4)
§
3
Рассмотрим производную от функции распределения по времени:
(5)
(последнее слагаемое в выражении производной обнуляется , т.к. )
Выражение для производной примет вид : (6)
(7)
скорость изменения функции распределения благодаря столкновениям, а величина
Величина называется интегралом столкновений, а уравнение вида (8) – кинетическим уравнением. Реальный смысл кинетическое уравнение (8) примет только после определения вида интеграла столкновений.
§ 3 Определение вида интеграла столкновений и уравнения Больцмана.
и
(10) (изменение числа частиц в единицу времени в фазовом объёме dVdГ )
(11)
и кинетического уравнения
Полученное интегрально - дифференциальное уравнение носит название уравнения Больцмана.
§ 3 Переход к макроскопическим уравнениям. Гидродинамическое уравнение непрерывности. Кинетическое уравнение Больцмана даёт микроскопическое описание эволюции состояния газа. Но на практике часто не требуется столь детально описывать процессы, поэтому при рассмотрении задач гидродинамики, задач о протекании процессов в неоднородных или сильно разреженных газах, задач о теплопроводности и диффузии газов и ряда других имеет смысл переходить к менее детальным (а следовательно более простым ) макроскопическим уравнениям. Такое описание применимо к газу, если его макроскопические свойства (температура, плотность, концентрация частиц, давление и т.п.) достаточно медленно меняются вдоль любого, произвольно выбранного направления в газе. Расстояния, на которых происходит существенное изменение макрокскопических параметров, должны значительно превышать длину свободного пробега молекул. В качестве примера рассмотрим рассмотрим способ получения гидродинамического уравнения.
Интегрирование производится по каждой из переменых , а значит можно, не меняя интеграла, произвести переобозначение переменных, например, во втором интеграле :
Отсюда немедленно получаем гидродинамическое уравнение непрерывности:
Задав в этом дифференциальном уравнении изменение плотности жидкости и считая жидкость несжимаемой, можно получить векторное поле направлений скоростей в любой точке жидкости.
§ 4. Слабо неоднородный газ. Теплопроводность газа.
Указанный интеграл обращается в нуль для функций вида
************************************************* § 4. Вычисление коэффициента теплопроводности одноатомного газа
§ 5. Пример решения кинетического уравненияМолекулы газа взаимодействуют по достаточно сложным законам. Это особенно касается реальных многоатомных газов. Сделанные допущения относительно характера поведения молекул газа позволяют упростить рассуждения (или даже сделать их в принципе возможными), но несколько удаляют нас от реальности. Сложные законы взаимодействия молекул, определяющие функцию в интеграле столкновений, не позволяют даже записать уравнение Больцмана для конкретных газов в точном виде. Даже при упрощении характера молекулярного взаимодействия математическая структура кинетического уравнения остаётся достаточно сложной, и нахождение его решения в аналитическом виде затруднительно. В кинетической теории газов применяют особые, более эффективные, чем попытка аналитического решения, методы приближенного решения уравнения Больцмана. В качестве примера рассмотрим одноатомный газ и задачу о теплопроводности.
а равновесная функция распределения примет вид . Эффективный метод приближённого решения уравнения ( ) основан на разложении искомых функций по полной системе взаимно ортогональных функций. В качестве таких функций рассмотрим полиномы Сонина, определяемые формклами :
В этой формуле r – произвольное, а s – целое положительное число либо нуль. В честноти
Решение уравнения ищем в виде следующего разложения
Умножим его с обеих сторон на и проинтегрируем по . Получим систему алгебраических уравнений, которая может быть решена на ЭВМ:
Для последнего выражения введены обозначения
Уравнение с l=0 отсутствует, поскольку в силу сохранения импульса
Об эффективности численного метода с применением разложения по полиномам Сонона можно судить по простоте правой части () и окончательному выражению (). Полученная в ходе решения басконечная система линейных алгбраических уравнений решается после искусственного усечения.
Заключение. Рассмотренный метод вывода кинетического уравнения Больцмана вполне удовлетворителен с физической точки зрения. Однако кинетическое уравнение может быть так же получено из математического аппарата, применяемого для описания движения частиц газа. В 1946 году такой вывод, получивший название динамического, бал дан Н. Н. Боголюбовым. Метод Боголюбова позволяет не только получить уравнение Больцмана, но и поправки к нему, т.е. члены следующих порядков по малому параметру газовости . Например, в указанном выводе учитывается одновременное столкновение только двух молекул и предполагается, что столкновения происходят в одной точке, т.е. являются локальными, и нет более или менее очевидного рецепта, позволяющего учесть столкновения групп из трёх, четырёх и большего числа частиц. Между тем ясно, что учёт подобных столкновений принципиально важен при рассмотрении плотных газов. В связи с этим целесообразно более строго подойти к выводу кинетического уравнения и к его возможным обобщениям. Метод Боголюбова позволяет учесть
Ñïèñîê ëèòåðàòóðû. 1. Å.Ì.Ëèôøèö, Ë.Ï.Ïèòàåâñêèé. Ôèçè÷åñêàÿ êèíåòèêà. Íàóêà, Ì., 1979 ã. 2. Þ.Á.Ðóìåð, Ì.Ø.Ðûâêèí. Òåðìîäèíàìèêà, ñòàòèñòè÷åñêàÿ ôèçèêà è êèíåòèêà. Íàóêà, Ì., 1972 ã.
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
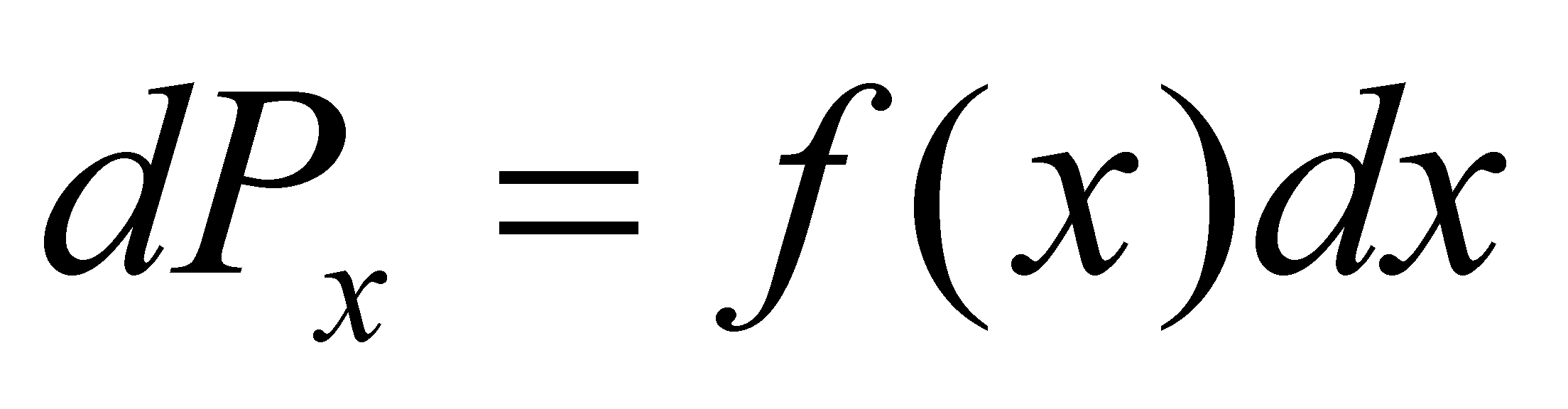

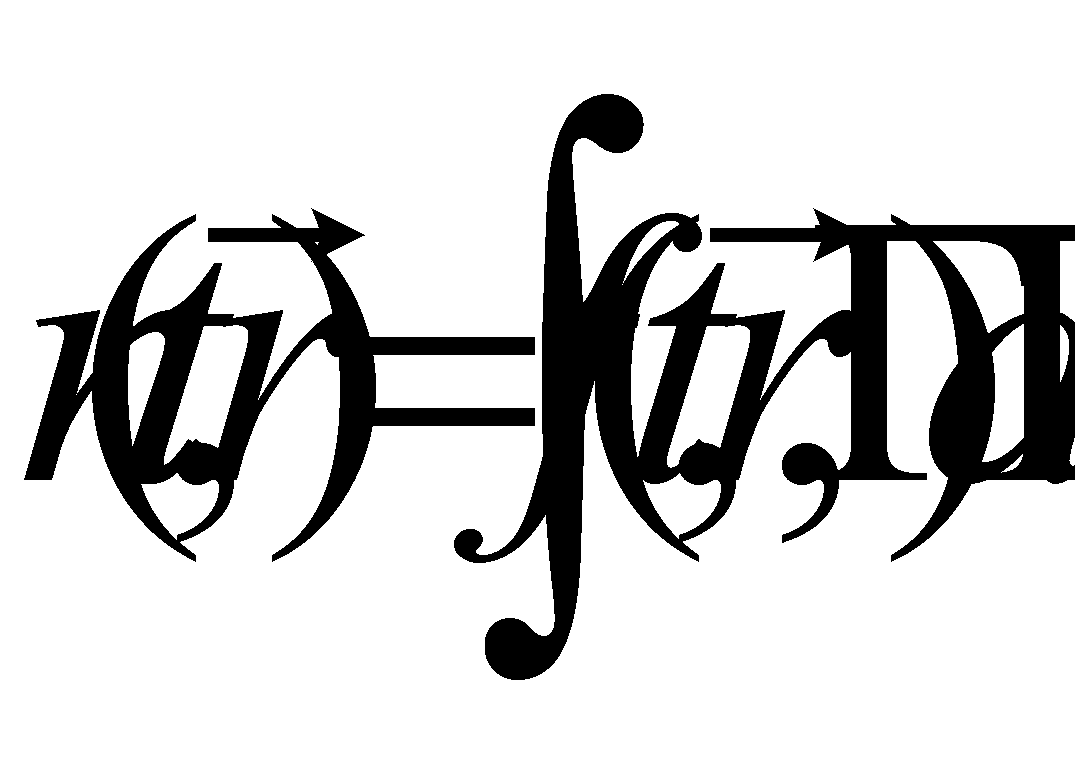

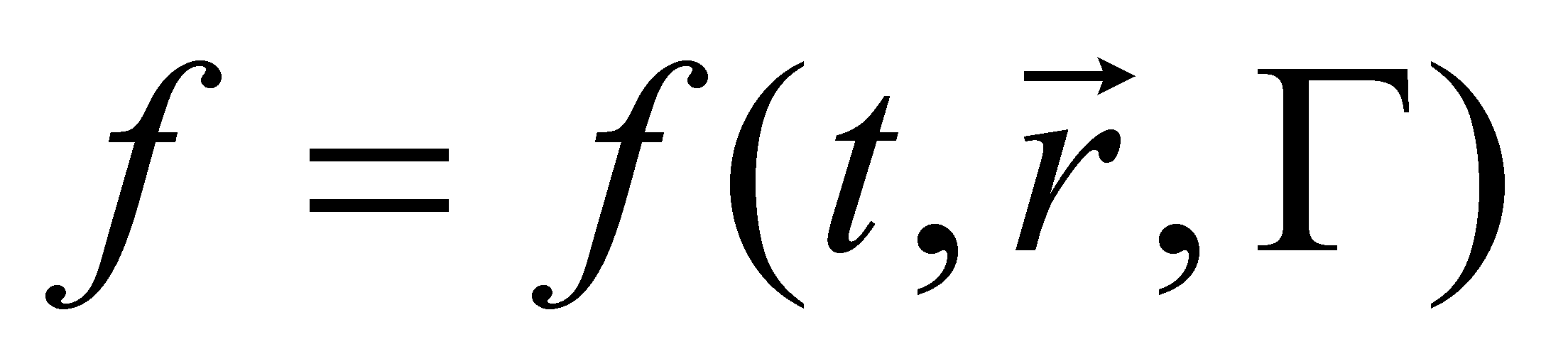

 Вывод кинетического уравнения.
Вывод кинетического уравнения.
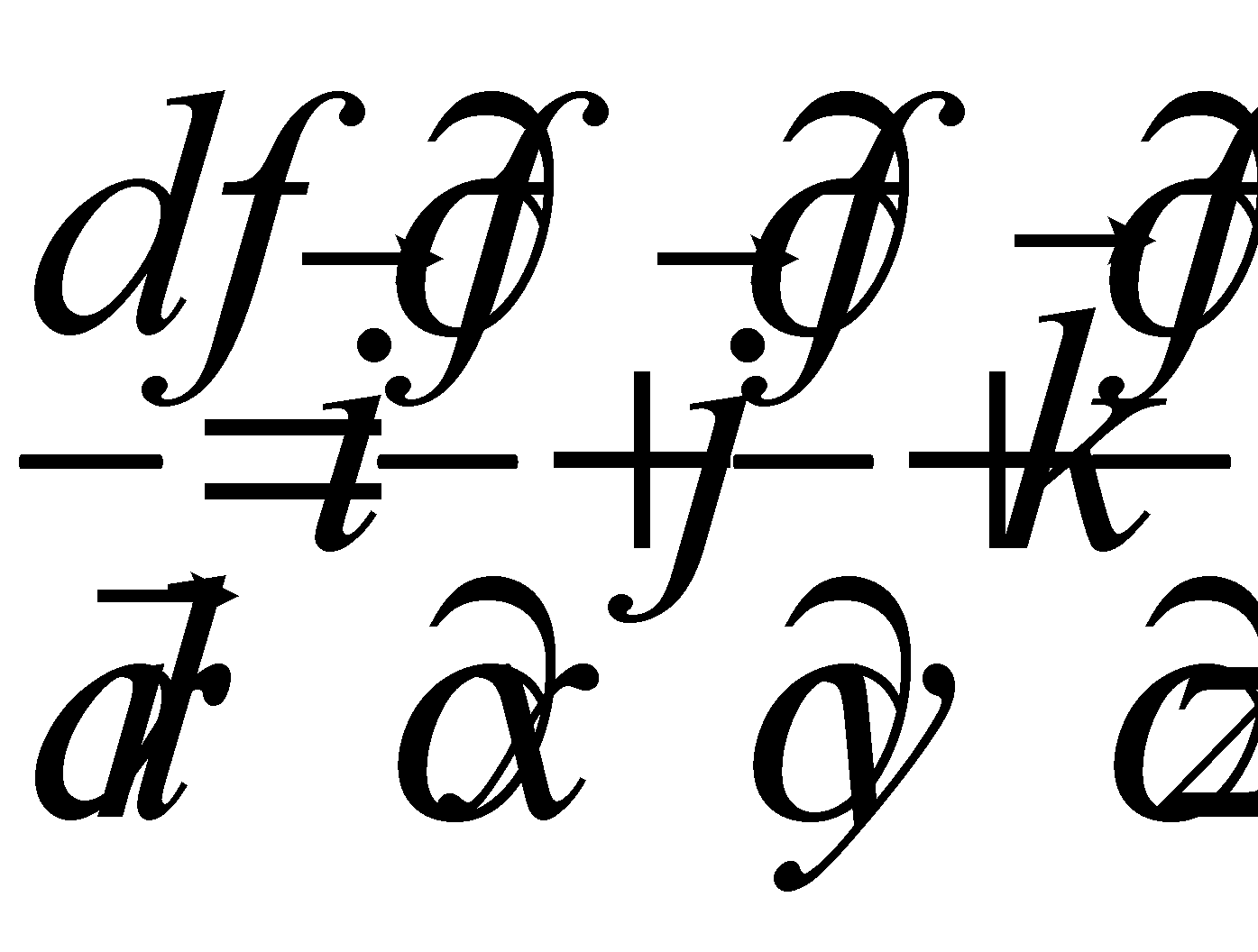
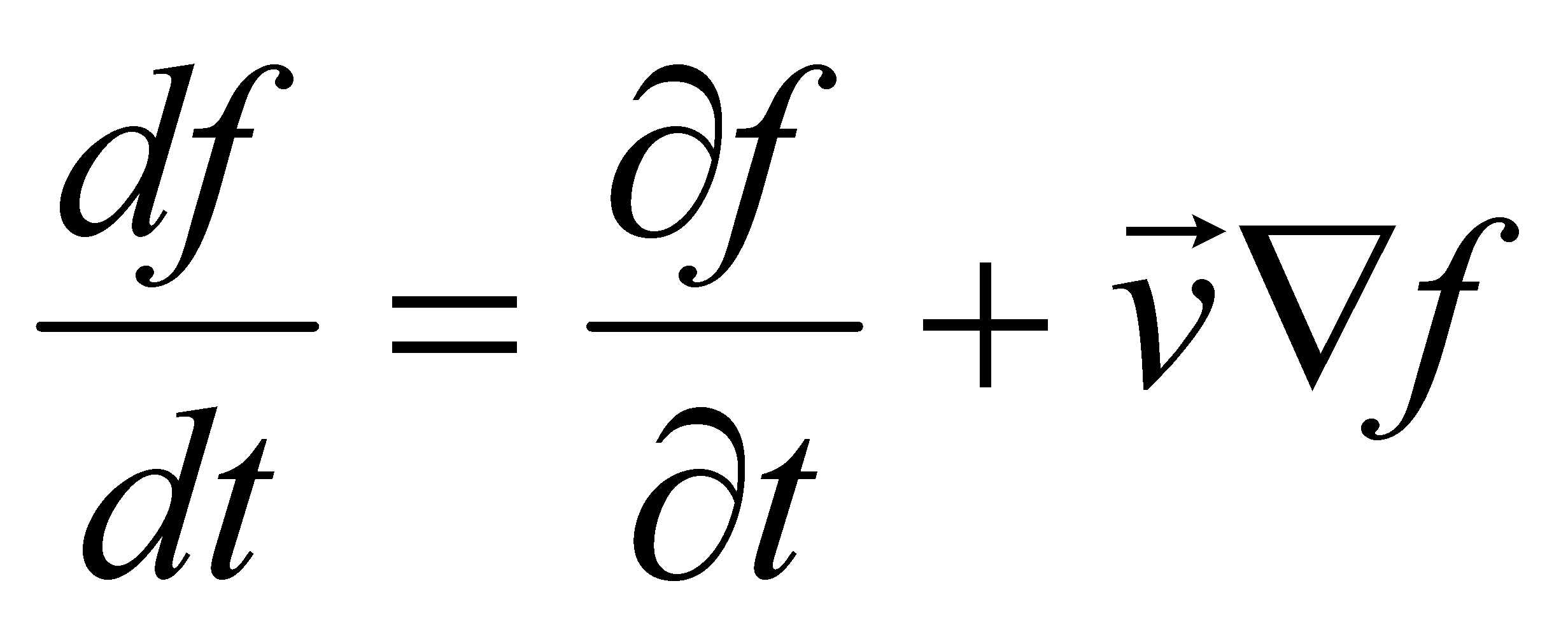
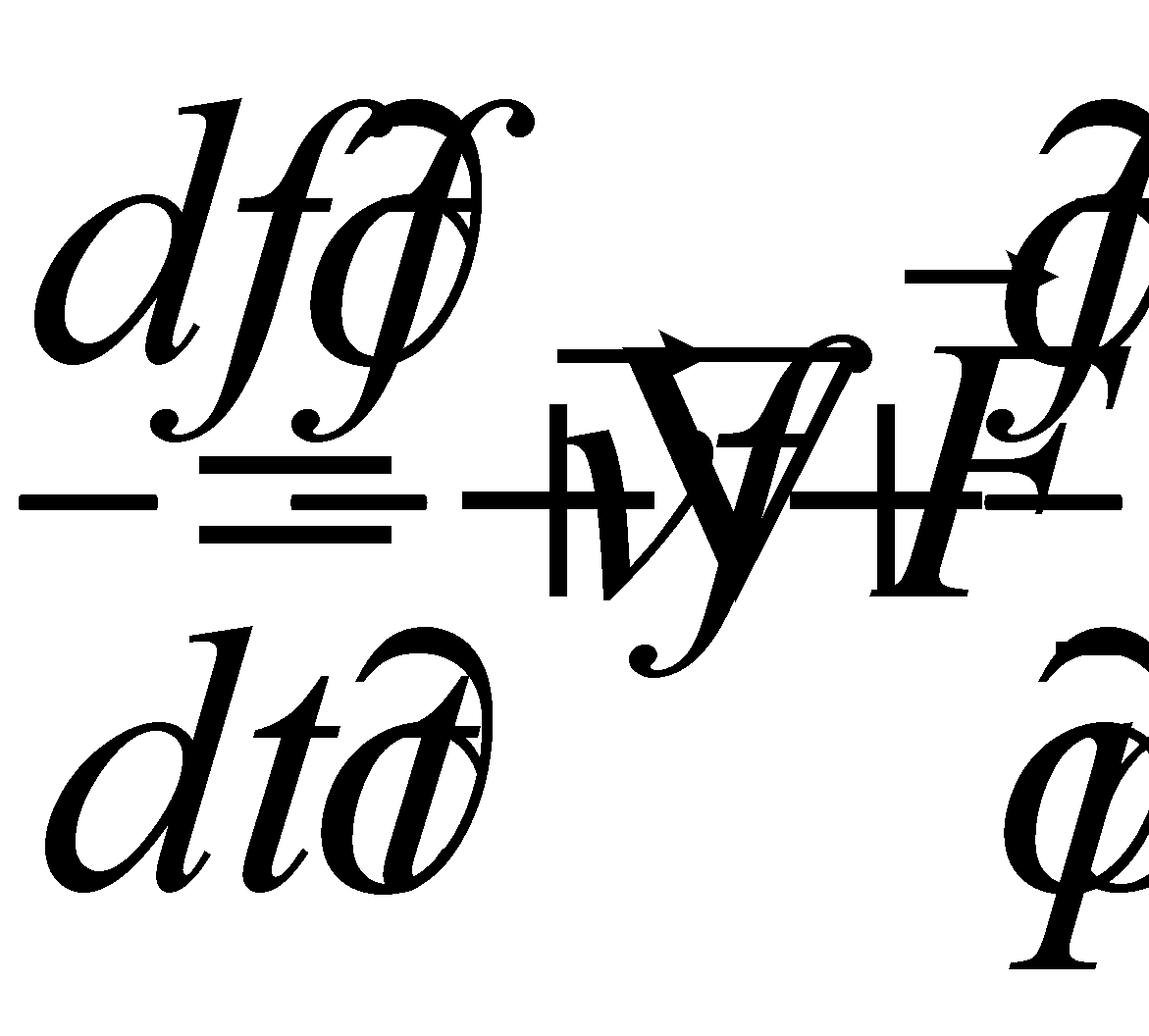
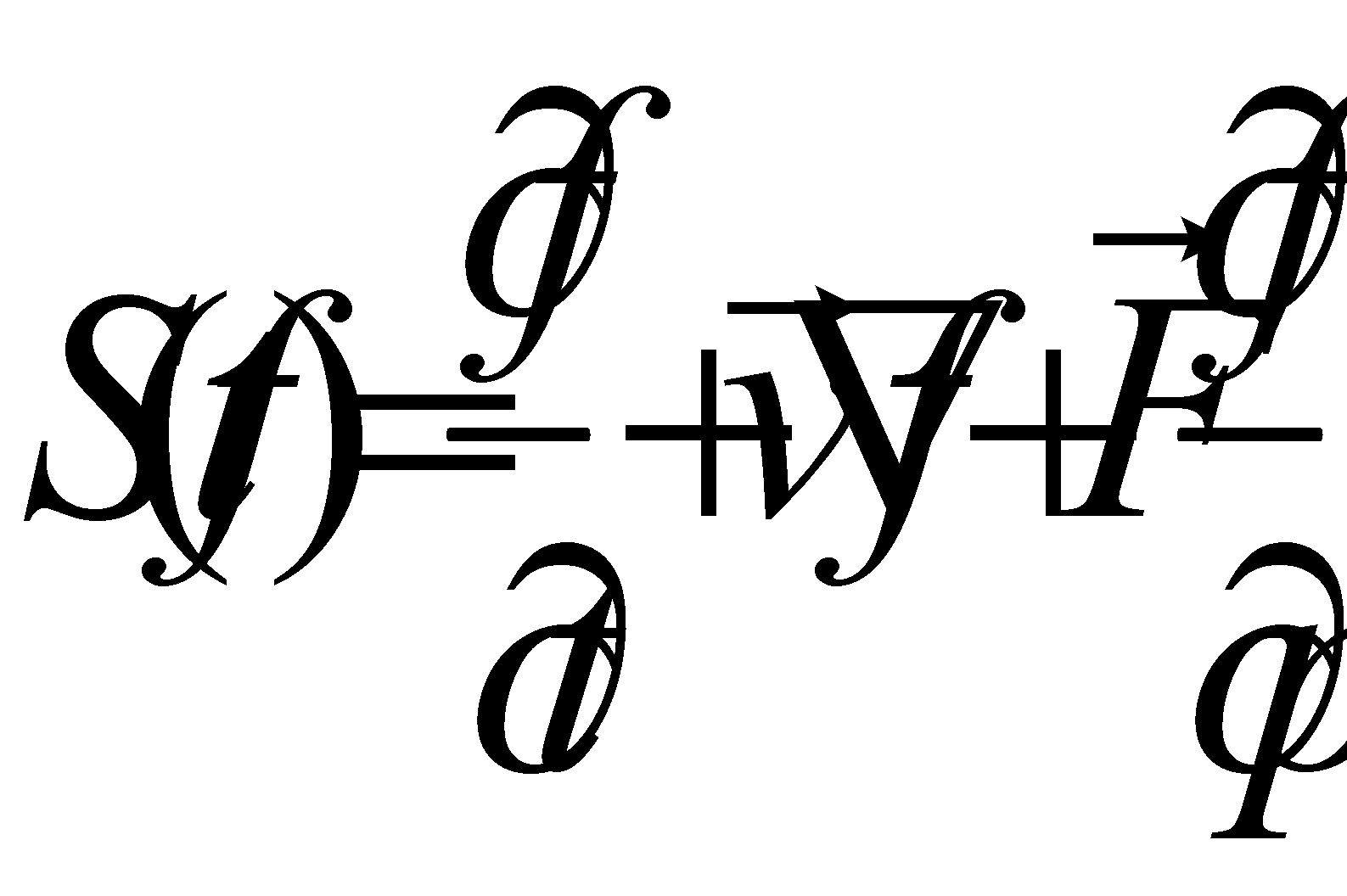
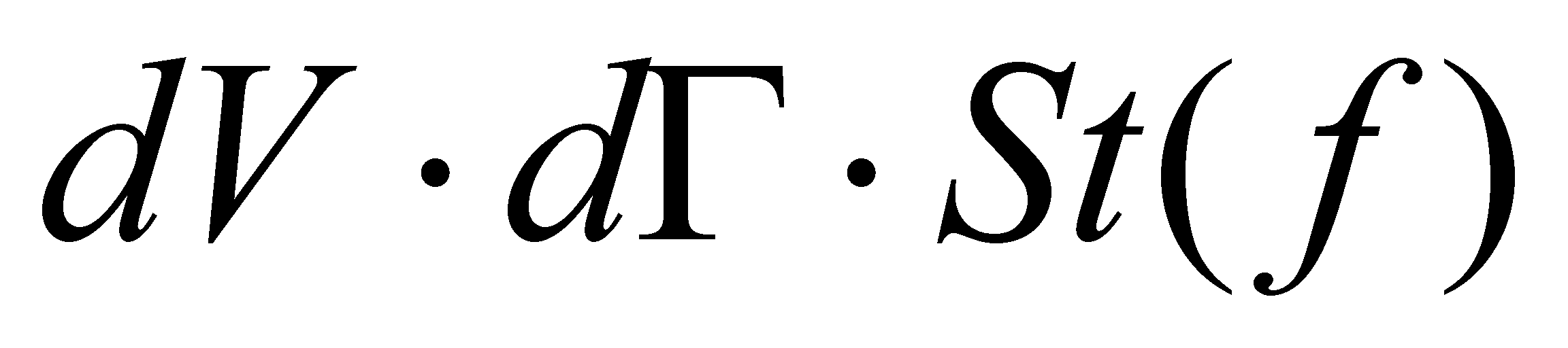
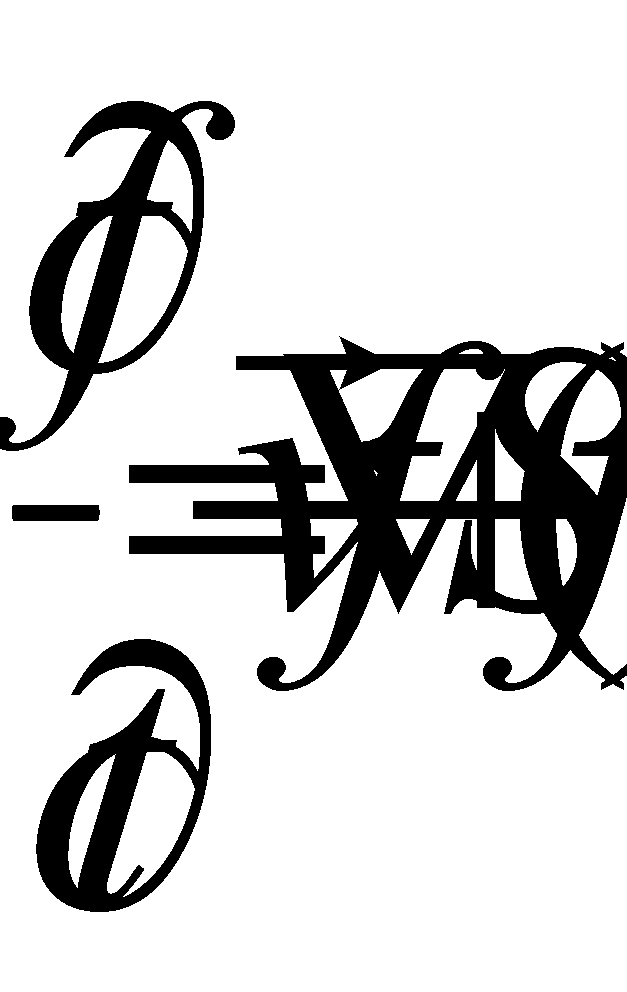
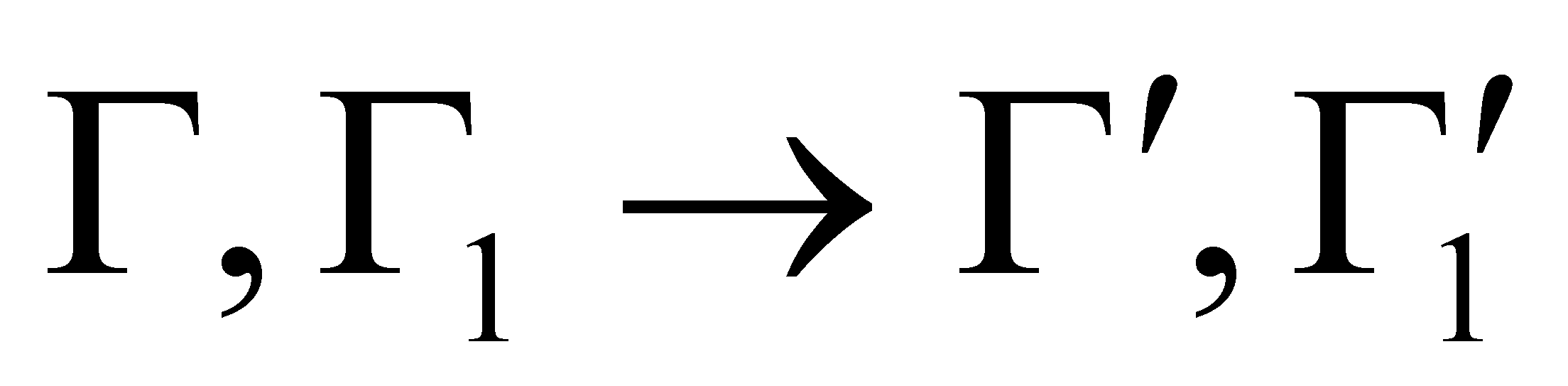

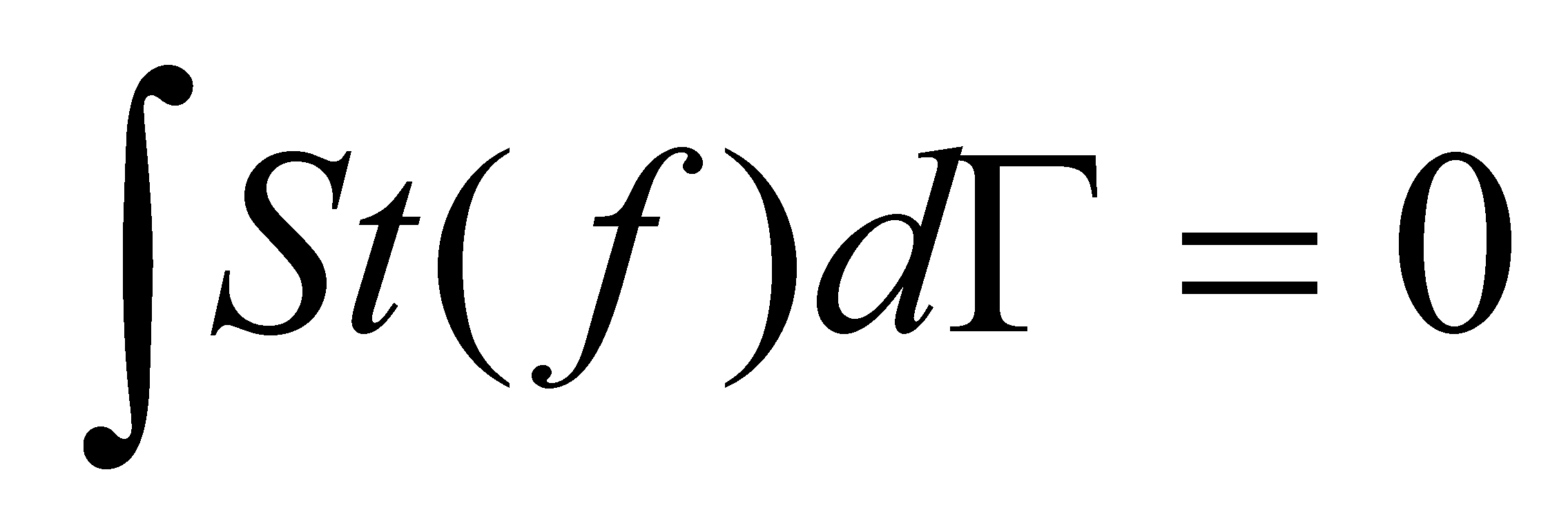
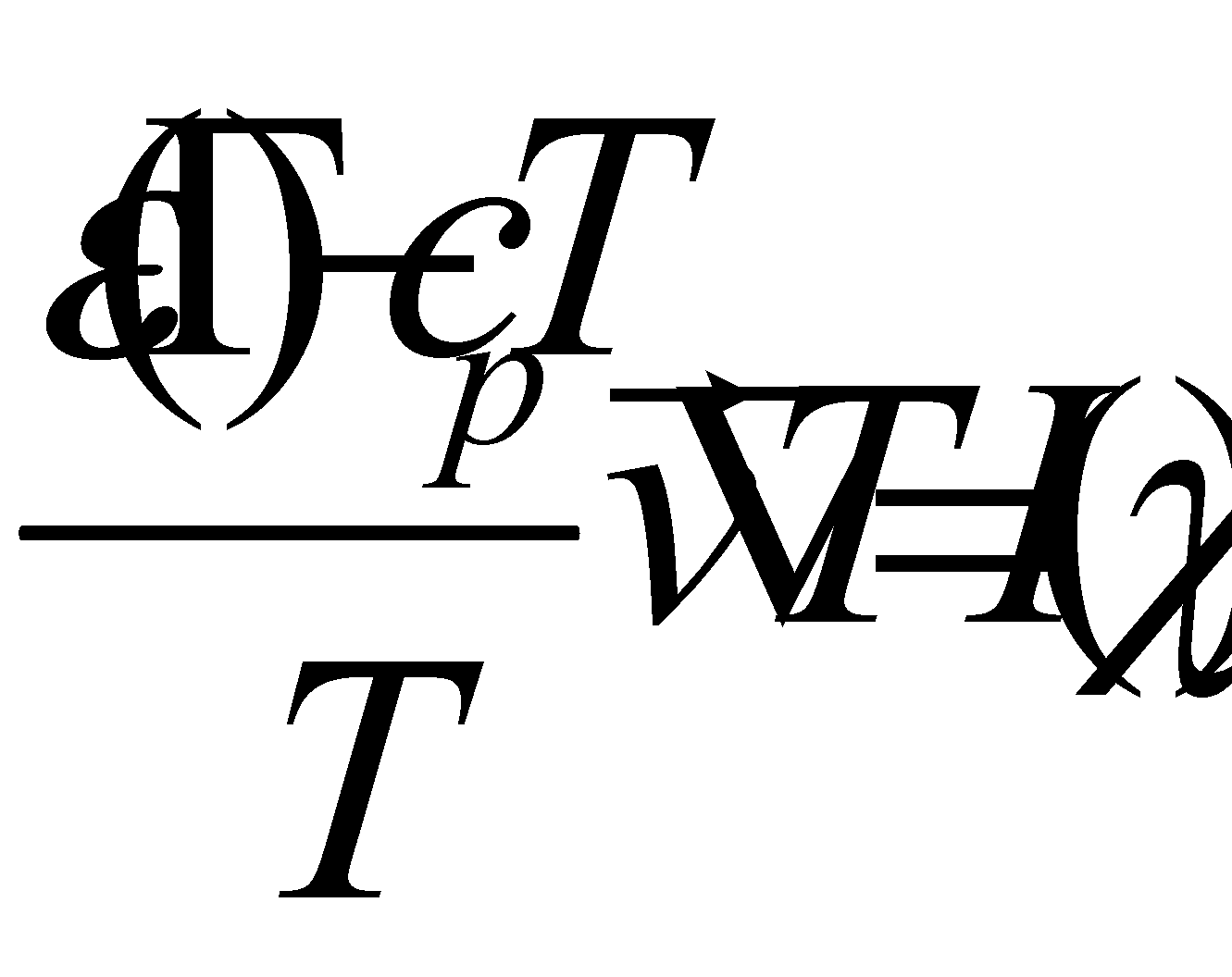
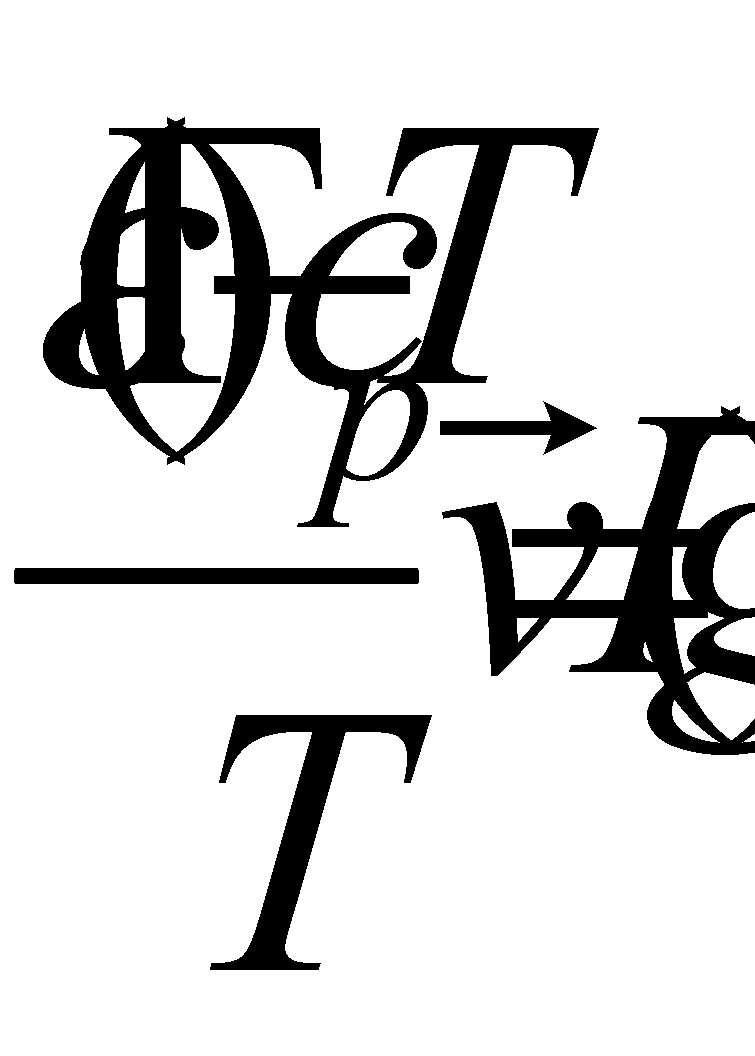

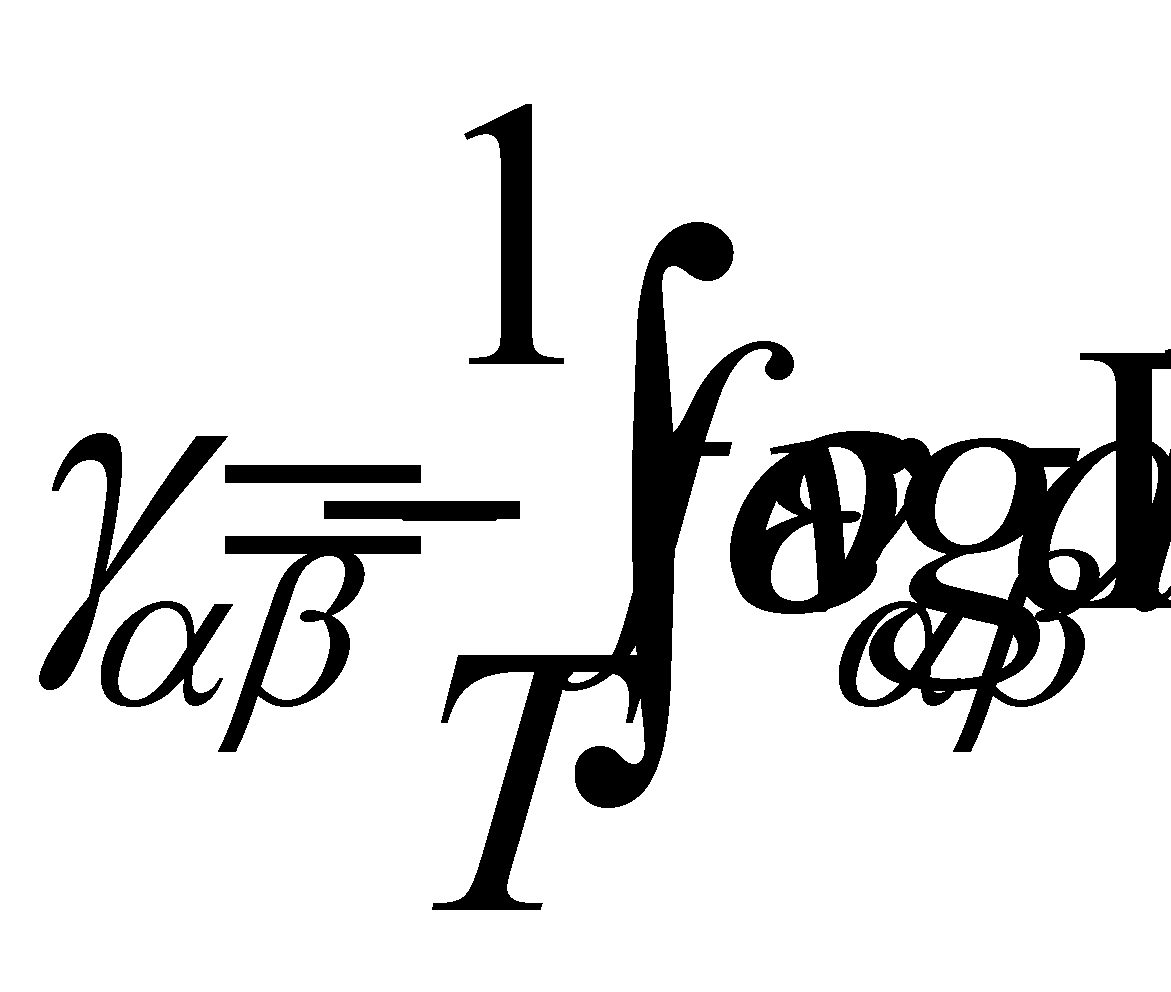
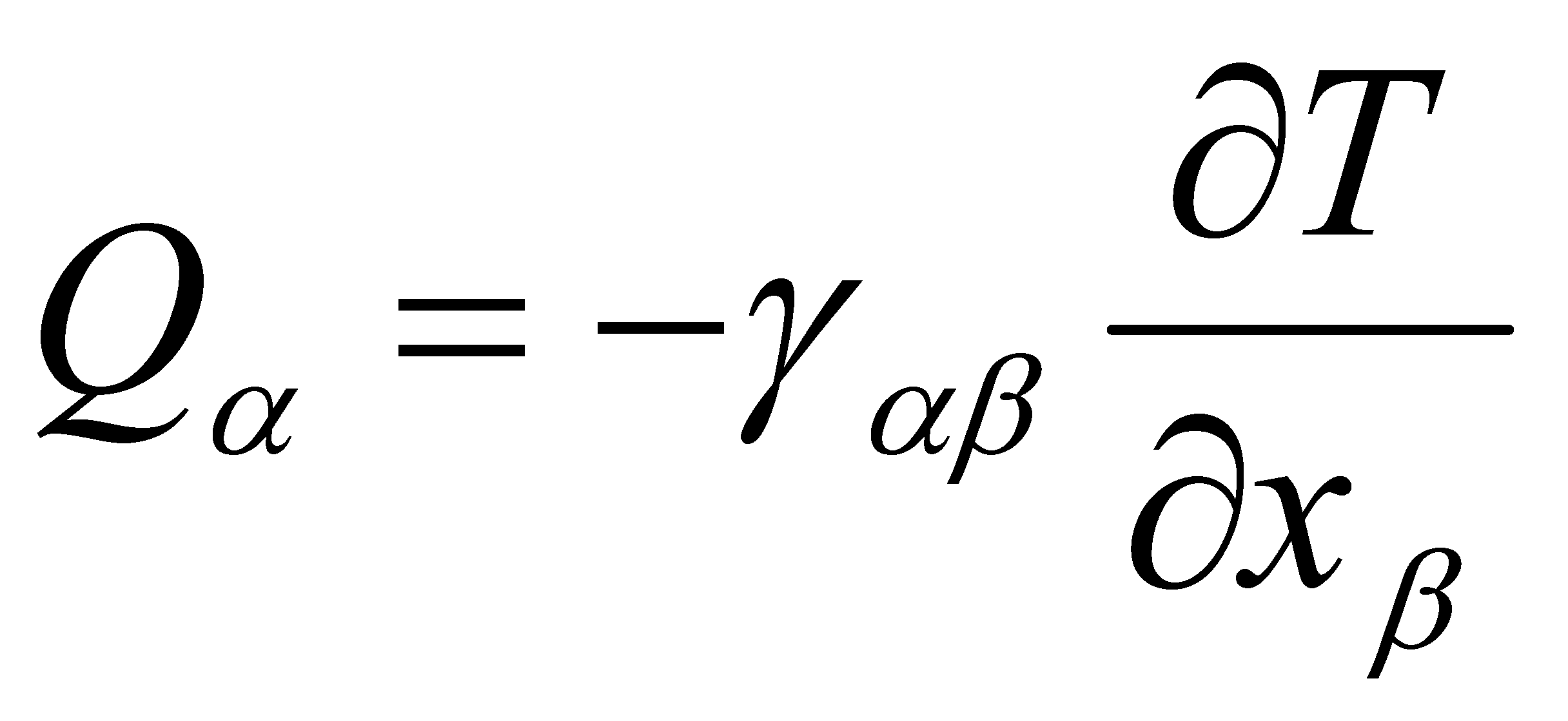
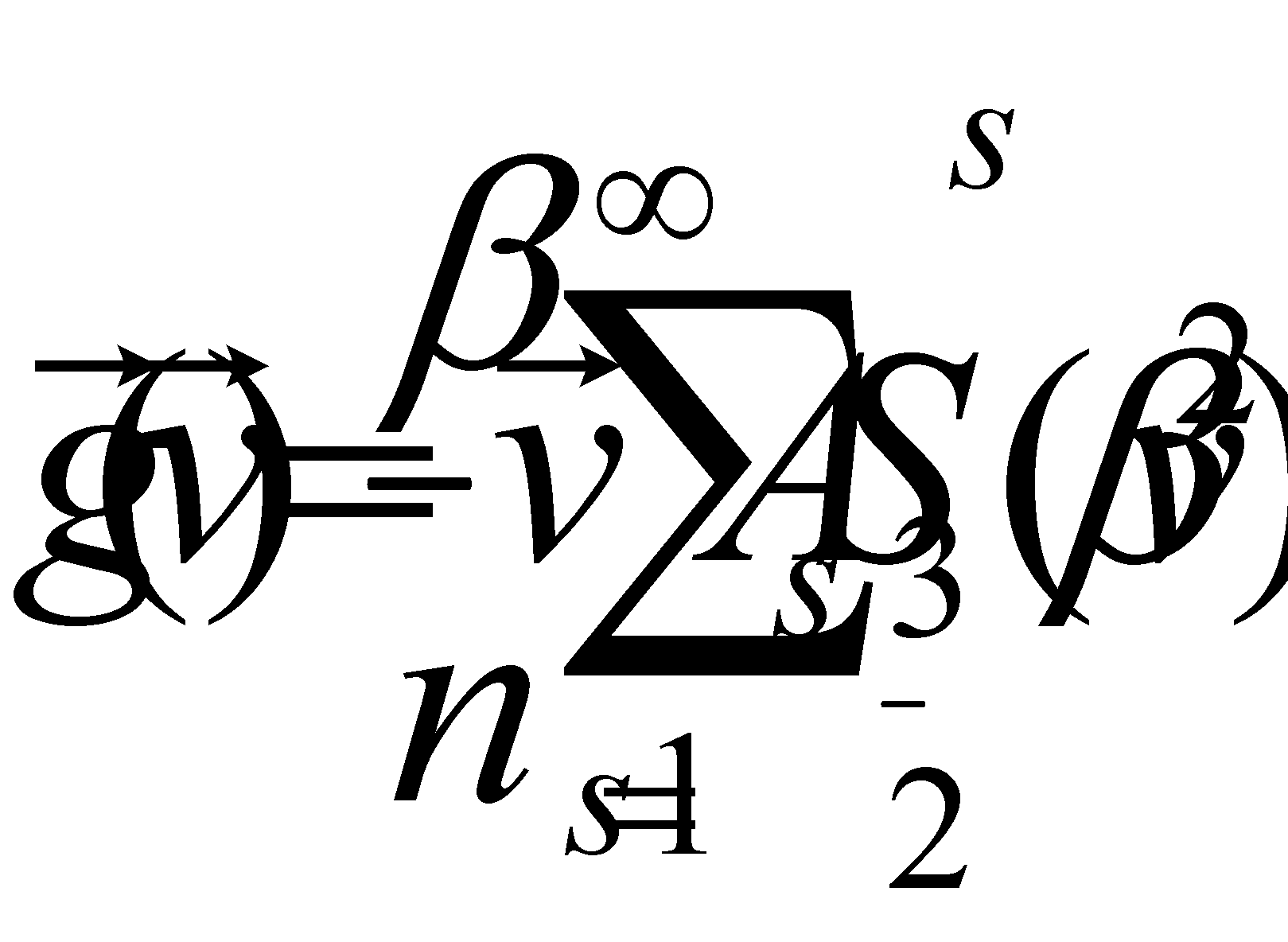
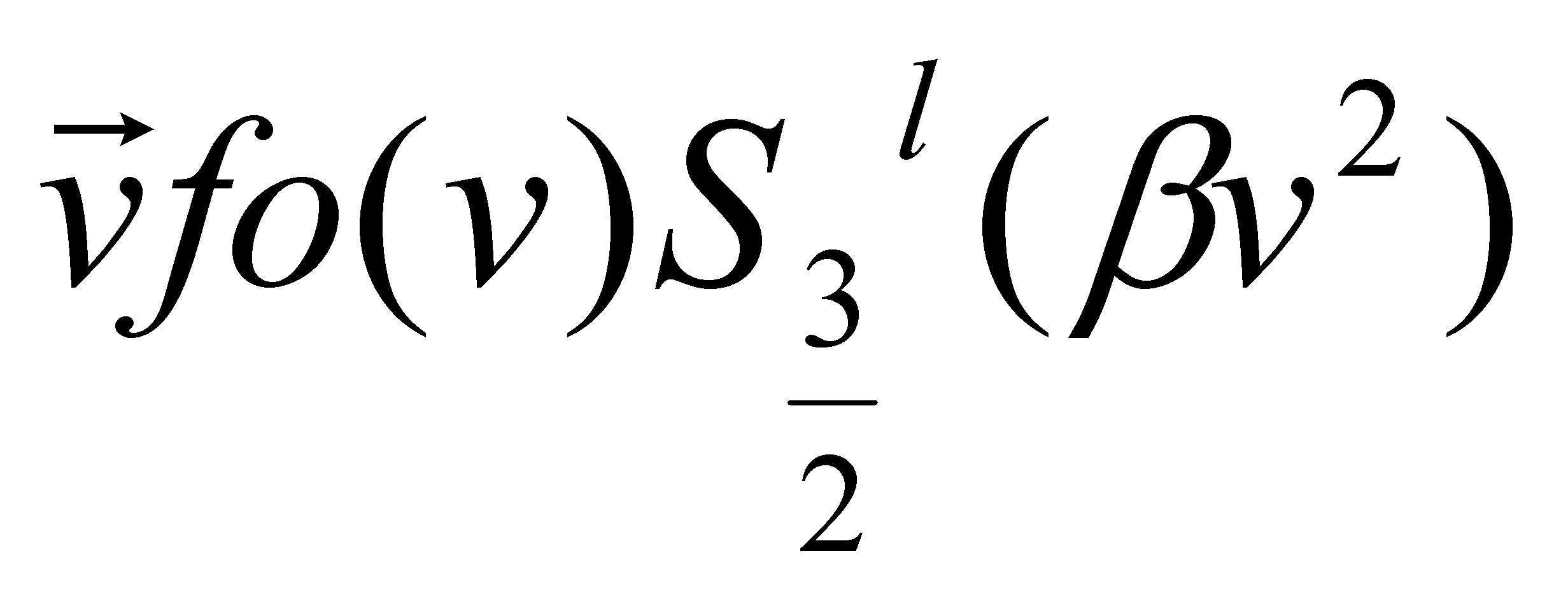
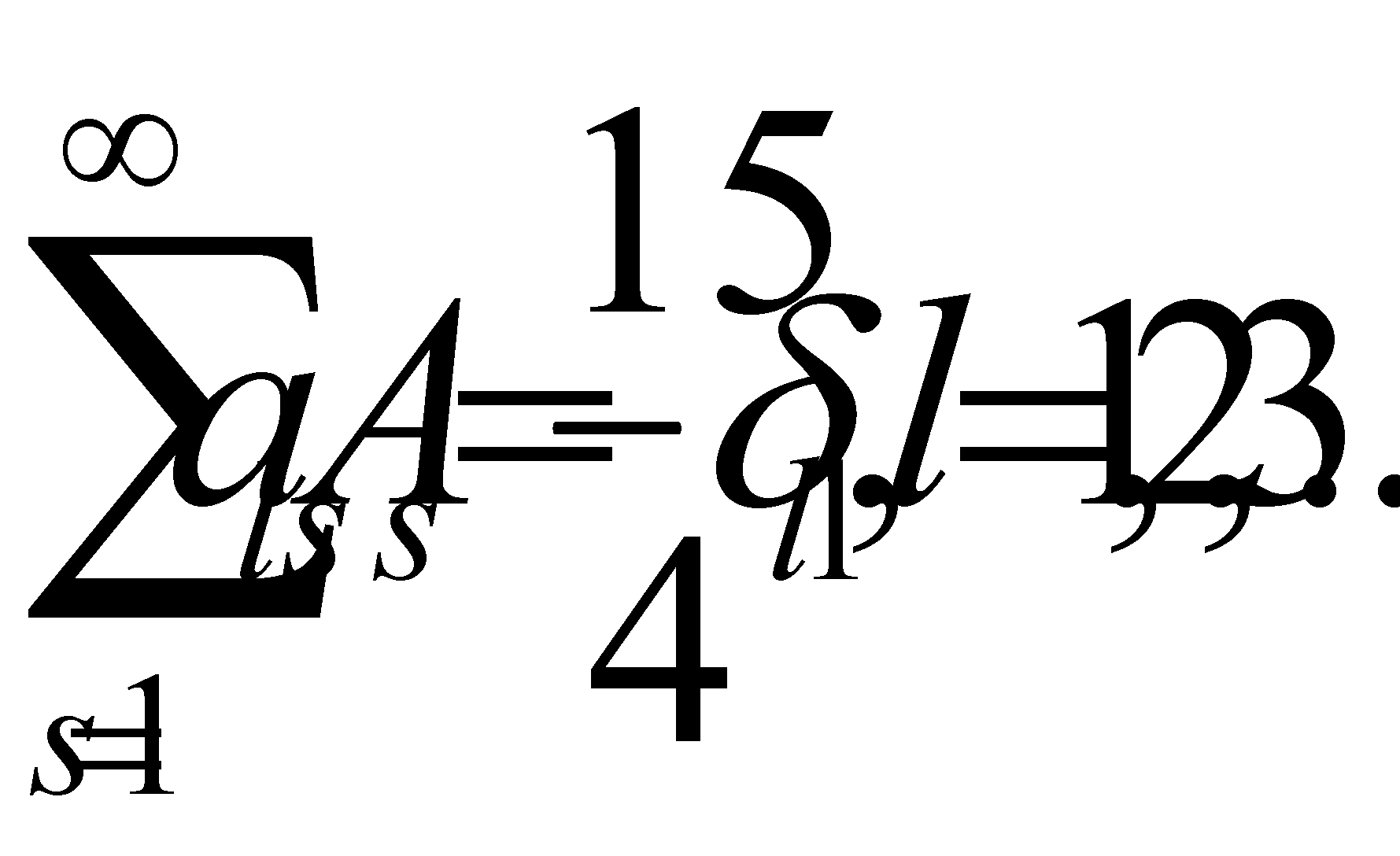

 Главная
Главная