Задача вихретокового контроля
Содержание 1. Техническое задание 2. Анализ технического задания 2.1 Прямая задача ВТК 2.2 Обратная задача ВТК 2.3 Модель задачи 2.4 Анализ литературы 2.4.1 Зарубежные методы решения 2.4.2 Отечественные методы решения 3. Прямая задача ВТК для НВТП 3.1 Уравнение Гельмгольца для векторного потенциала 3.2 Поле витка над многослойной средой 3.3 Воздействие проводящего ОК на НВТП 4. Обратная задача ВТК для НВТП 5. Некорректные задачи 5.1 Основные определения. Корректность по Адамару 5.2 Корректность по Тихонову 5.3 Вариационные методы решения некорректных задач 5.3.1 Метод регуляризации 5.3.2 Метод квазирешений 5.3.3 Метод невязки 6. Нелинейное программирование 6.1 Метод штрафных функций 6.2 Релаксационные методы 6.2.1 Метод условного градиента 6.2.2 Метод проекции градиента 6.2.3 Метод случайного спуска 6.3 Метод множителей Лагранжа 7. Линейное программирование 7.1 Алгоритм симплексного метода 8. Одномерная минимизация 8.1 Алгоритм методов 9. Результаты численного моделирования 9.1 Аппроксимации при численном моделировании 9.2 Модели реальных распределений электропроводности 9.3 Принципиальная возможность восстановления 9.4 Восстановление по зашумленным данным 9.5 Восстановление с учетом дополнительной информации 9.6 Восстановление при различном возбуждении 10. Заключение 11. Литература Приложение 1 - Программная реализация Приложение 2 - Удельная электропроводность материалов Приложение 3 - Результаты восстановления Приложение 4 - Abstract
1. Техническое задание Разработать алгоритм решения обратной задачи вихретокового контроля (ВТК). Объектом контроля (ОК) являются проводящие немагнитные листы. Объекты контроля подвергаются термообработке (закалка, отпуск) или насыщению внешних слоев различными веществами, что приводит к изменению механических, а вследствие этого и электромагнитных свойств материала листа по глубине. Задача заключается в определении, в рамках допустимой погрешности, зависимости электропроводности (ЭП) от глубины s (Н) в ОК для данного состояния. Метод контроля заключается в измерении определенного количества комплексных значений вносимой ЭДС на различных частотах с помощью накладного вихретокового преобразователя (НВТП). Необходимо выбрать математическую модель задачи, способ аппроксимации искомого решения, рассмотреть алгоритм решения. Используя программную реализацию, исследовать поведение погрешности аппроксимации зависимости s (Н) от следующих факторов:
2. Анализ технического задания. Основная задача вихретокового контроля с помощью накладных преобразователей состоит из двух подзадач:
2.1 Прямая задача ВТК Полагая зависимость ЭП от глубины известной проведем ее кусочно-постоянную аппроксимацию. Это позволяет свести исходную задачу к расчету ЭДС в многослойном листе, в каждом слое которого ЭП принимает постоянное значение. Как показано в работе [50], подобная модель вполне адекватно описывает задачу и дает отличное согласование с результатами опытов. Рекуррентные формулы для произвольного количества слоев хорошо известны [1-5,36, 42,43,50-52]. Таким образом решение прямой задачи в рамках принятой модели затруднений не вызывает. 2.2 Обратная задача ВТК С математической точки зрения обратная задача ВТК относится к классу некорректных задач[49] и ее решение неустойчиво т.е. при сколь угодно малой погрешности исходных данных( набора измеренных вносимых ЭДС ) погрешность решения ( рассчитанных локальных значений ЭП ) может быть сколь угодно большой, а одному набору измерений может отвечать много (формально бесконечно много) распределений ЭП по глубине. При попытке расчета некорректной задачи как корректной, вычислительный процесс за счет неустойчивости сваливается в заведомо худшую сторону. В нашем случае это означает получение распределения ЭП, которое, хотя и обеспечивает требуемое совпадение измеренной и вычисленной ЭДС, но является явно нереальным из-за осцилляций. Следует отметить, что амплитуда и частота осцилляций распределения ЭП растут при увеличении числа независимых параметров аппроксимации ЭП ( коэффициентов полинома в случае полиномиальной аппроксимации, количества узлов при сплайн-аппроксимации и т.д.). При наличии погрешности измерения вносимой ЭДС, превышающей на несколько порядков вычислительную погрешность и на практике составляющей не менее (0.5-1)% от измеряемого сигнала, ситуация значительно осложняется. Учитывая вышеизложенное для выделения из множества допустимых распределений решения, наиболее удовлетворяющего физической реальности, в алгоритмах решения обратной задачи необходимо использовать дополнительную априорную информацию. На практике это реализуется введением некоторых критериев, позволяющих отличить решение, отвечающее практике, от физически нереального. Для решения обратной задачи ВТК предлагались три возможные стратегии[46]:
В нашем случае остановимся на втором подходе, поскольку он сочетает в себе универсальность, точность и относительную простоту реализации. В целом процесс решения обратной задачи сводится к итерационному решению прямой задачи для текущей оценки распределения ЭП и внесению изменений в эту оценку в соответствии с величиной невязки. 2.3 Модель задачи Приведем основные положения, на основе которых будет построена модель нашей задачи:
2.4 Анализ литературы 2.4.1 Зарубежные методы решения Решению обратной задачи ВТК посвящен ряд работ в зарубежных изданиях. Следует отметить монографию [38], в которой рассмотрены случаи импульсного возбуждения, а оперируют в частотной и временной областях напряженностью электрического поля. Подход к решению квазистационарных задач рассмотрен в цикле статей [45-51]. Он основан на интегральной постановке задачи с помощью функций Грина[31-34,39]. Для иллюстрации рассмотрим решение обратной задачи ВТК согласно [49]. А. Прямая задача Определим функцию v(r)=( s (r) - s 0 )/ s 0 , где s (r) - произвольное распределение проводимости, а s 0 - ее базовая величина. Функция v(r) может представлять собой как описание произвольного распределения проводимости (в этом случае для удобства полагаем s (r)= s 0 вне некоторого ОК объема V , тогда v(r) отлична от нуля только в пределах V ) так и некоторого дефекта (для трещины v(r)=-1 внутри дефекта и равна нулю вне его). Рассмотрим систему уравнений Максвелла в предположении гармонического возбуждения exp(-jwt) и пренебрегая токами смещения:
где P(r)=[ s (r)- s 0 ] Ч E(r)= s 0 Ч v(r) Ч E(r) - может интерпретироваться как плотность диполей эффективного тока, причиной которого является вариация s (r)- s 0 . Решение уравнений Максвелла можно представить в виде
где E i (r) - возбуждающее поле, а G(r|r’) - функция Грина, удовлетворяющая уравнению С ґ С ґ G(r|r’)+k 2 Ч G(r|r’)= d (r-r’) , k 2 =-j Ч w Ч m 0 Ч s 0 , d (r-r’) - трехмерная дельта-функция. Импеданс ВТП можно выразить как
где интеграл берется по измерительной катушке, J(r) - плотность тока в возбуждающей катушке. Применяя теорему взаимности импеданс можно представить через возбуждающее поле:
где интеграл берется по объему ОК. В. Обратная задача Пусть v(r) - оценка истинной функции v true (r) , Z obs (m) - измеренный импеданс ВТП в точке r 0 на частоте возбуждения w , m=(r 0 , w ) - вектор в некоторой области определения M , Z[m,v] - оценка величины Z obs (m) на основе решения прямой задачи. Определим функционал невязки измеренных и рассчитанных значений импеданса ВТП как :
Предположим, что для решения обратной задачи используется итерационный алгоритм типа метода спуска: v n (r)= v n-1 (r)+ a s n (r) . Можно показать, что в случае метода наискорейшего спуска итерация имеет вид: v n (r)= v n-1 (r)- a Ч С F[ v n-1 (r) ] , где градиент функционала С F[v] можно определить как :
где Re обозначает вещественную часть, * обозначает комплексную сопряженность. Требуемый в (2.4.6) градиент импеданса можно определить как:
где E * (r) - решение уравнения
С. Аппроксимация при решении обратной задачи Пусть электропроводность моделируется с помощью конечного числа переменных (например узловых значений некоторой аппроксимации), а вектор р состоит из этих переменных. Тогда выражение (2.4.7) принимает вид:
где ( С Z) j - j -ая компонента градиента импеданса. Значение j-ой компоненты градиента невязки (2.4.6) можно представить как:
Следует обратить внимание на то, что в случае дискретного пространства М (конечное число измерений) интеграл в (2.4.10) заменяется суммой. С учетом приведенных преобразований итерация метода наискорейшего спуска принимает вид:
где n - номер итерации. D. Пример применения В качестве примера рассмотрим функцию v(r) в виде v(r)= S c i Ч f i (r) , i=1,N , где f i (r) - множество линейно независимых базовых функций с коэффициентами c i . Рассматривая коэффициенты c i в роли параметров аппроксимации ( c i =p i ) получим из (2.4.9) для компонентов градиента импеданса:
В случае проводящего ОК, состоящего из N параллельных слоев с проводимостью s j распределение электропроводности по глубине можно представить с помощью функций Хевисайда H(z) как s (z)= S s j Ч [ H( z-z j ) - H( z-z j+1 ) ] . Подставляя в (2.4.12) базовые функции вида f i (z)=[H( z-z j )-H( z-z j+1 )] , получим окончательное выражение:
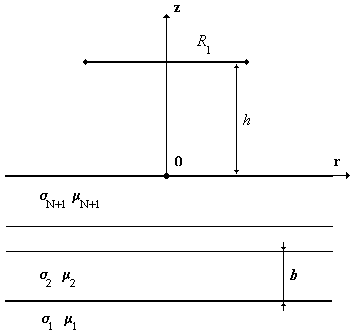
Отметим основное преимущество такого решения. Несмотря на определенную сложность вычислений при решении интегральных уравнений (2.4.2-2.4.8) для расчета градиента импеданса НВТП необходимо решить только две такие задачи. 2.4.2 Отечественные методы решения Подход, в значительной мере аналогичный работам [45-51] был предложен в работе [41]. Из-за небольшого объема в ней уделено недостсточное внимание вопросам практической реализации, объяснены не все обозначения и не приведены результаты численного моделирования. В целом это значительно снижает практическую ценность статьи. Приведем основные положения этой работы. Прямая задача Пусть круговой виток радиусом а с током I находится в точке P=P s (r, j ,z), j О (- p , p ) вблизи немагнитного ОК, занимающего область V . Пусть ОК обладает электрической проводимостью s = s 0 Ч s (Р) являющейся произвольной функцией координат. Требуется по N измерениям величины э.д.с. определить s как функцию координат точек P О V . Причем i -ое измерение э.д.с. будем проводить на i -ом измерительном круговом витке с координатами P i =P i (r, j ,z) i=1,N при неизменных частоте и расположении возбуждающего витка. В общем случае напряженность электрического поля Е определяется через векторный магнитный потенциал А , причем А = А 0 + А вн , где А 0 - возбуждающий, а А вн - вносимый потенциалы.
Вводя функцию Грина G(p,p 0 ) получим
При этом вносимая напряженность электрического поля
Вносимая э.д.с., наводимая в i -ом витке
где функция Грина G(P,P 0 ) имеет вид
В дальнейшем рассмотрим случай, при котором V -полупространство (r>0,\ j \< p ,z<0) с электрической проводимостью s = s 0 Ч s (Р) , где s (Р) - произвольная функция координаты z . В этом случае выражение (2.4.17) примет вид
где k 2 =jw m 0 s 0 . Для напряженности электрического поля Е(Р) справедливо представление
где Е 0 (р) - возбуждающее поле витка. После проведения серии из N измерений величины e вн выражение (2.4.19) дает связь между вносимыми ЭДС e i и s (z)E(r,z) . Чтобы определить непосредственно s = s (z) , находим E(r,z) при известной функции s (z)E(r,z) из (2.4.20), после чего исключаем E(r,z) из известного. Обозначим x(p)=-k 2 s (z)E(r,z) , а измеряемую совокупность ЭДС через Fi . Тогда (2.4.19) можно записать в операторной форме как
где d - погрешность измерения. Обратная задача Построим функционал Ф(х)=||F-Px|| 2 + a ||x-x 0 || 2 , где х 0 - некоторое известное І близкое І к искомому распределение, удовлетворяющее F 0 =Px 0 . Образуем вариацию функционала Ф(х) , используя определение сопряженного оператора (Px,y)=(x,P*y) . Для нахождения минимума Ф(х) приравняем его вариацию d Ф нулю. Вводя вспомогательную функцию u=x-x 0 и учитывая F 0 =Px 0 проведем ряд преобразований. Искомое распределение s (z) можно найти из равенства
где напряженность электрического поля в точке р для известного распределения s (z) имеет вид
Система алгебраических уравнений для определения коэффициентов С i имеет вид
3.1 Уравнение Гельмгольца для векторного потенциала Взаимодействие преобразователя с объектом контроля определяется системой уравнений Максвелла в дифференциальной форме[6] :
где
Дополним систему (3.1) уравнениями связи:
где
Преобразуем систему уравнений (3.1) с учетом следующих предположений[4] :
Поскольку ротор градиента любого скаляра тождественно равен нулю, величину в скобках выражения (3.4.2) можно приравнять градиенту некоторого скаляра y , например скалярного потенциала электрического поля :
Заменяя векторы напряженности магнитного и электрического поля в (3.4.1) через векторный потенциал магнитного поля получаем :
Откуда после очевидных преобразований следует:
где
Поскольку векторный потенциал магнитного поля задан с точностью до градиента некоторого скаляра, а потенциал y с точностью до постоянной величины, имеется возможность положить значение величины в квадратных скобках выражения (3.7) равное нулю (так называемая калибровка Лоренца). В результате получаем уравнение Гельмгольца для векторного потенциала магнитного поля :
В дальнейших рассуждениях используем следующие предположения :
. 3.2 Поле витка над многослойной средой
В цилиндрической системе координат выражение (3.9) имеет следующий вид :
Применяя к (3.10) преобразование Фурье-Бесселя с ядром в виде функции Бесселя первого порядка имеющее вид :
Так как на поверхностях раздела слоев ОК должна сохранятся непрерывность тангенциальных составляющих векторов напряженностей магнитного и электрического поля, дополняем уравнение (3.11) граничными условиями на поверхностях слоев ОК( граничные условия одинаковы для А и А* ) :
Решив уравнение (3.11) с учетом граничных условий (3.12-3.13) и применяя к решению обратное преобразование Фурье-Бесселя имеющее вид :
где j = j ( l , m , s ) - функция граничных условий. 3.3 Воздействие проводящего ОК на НВТП Для большинства инженерных расчетов можно использовать нитевидную модель обмоток НВТП использованную в (п 3.2). При данном упрощении получаем :
Анализируя формулу (3.14) можно заметить, что первый интеграл представляет собой векторный потенциал создаваемый возбуждающей обмоткой, а второй интеграл - векторный потенциал вносимый ОК. В практике ВТК обычно анализируются вносимые параметры НВТП (напряжение, импеданс) поэтому получим выражение для вычисления вносимого напряжение кругового трансформаторного накладного ВТП используя (3.15-3.16):
Подставляя выражение для вносимого векторного потенциала (3.14) в уравнение (3.17) окончательно получаем :
где
Функция граничных условий для m -слойного ОК с плоскопараллельными слоями может быть вычислена по рекуррентной формуле[2]:
где
При анализе годографов для удобства используют нормированные зависимости. Для НВТП нормировку производят по модулю максимального вносимого напряжения, которое соответствует идеально проводящему ОК и вычисляется при j м = -1 :
Такая нормировка обобщает полученные результаты, расширяет область их применения и делает их однозначными. Отметим, что для получения часто используемого в ВТК значения импеданса НВТП достаточно разделить правую часть (3.18) на величину тока возбуждения I .
4. Обратная задача ВТК для НВТП Решение обратной задачи ВТК состоит в нахождении зависимости s (h) распределения электропроводности по глубине пластины используя набор из N измеренных с помощью НВТП вносимых напряжений. Математически обратную задачу можно представить интегральным уравнением
Поскольку явного метода решения уравнения (4.1) не существует, применим к нему метод квазирешения (п5.3.2). В постановке для локального в смысле Чебышева критерия получим корректную задачу минимизации функционала невязки:
Учет априорной информации в обратной задачи ВТК удобно проводить в виде интервала [ s min , s max ], которому могут принадлежать значения электропроводности. В этом случае можно рассматривать задачу (4.2) как задачу нелинейного программирования вида:
Заметим, что поскольку ограничения в задаче (4.3) являются линейными, разумным представляется применение метода условного градиента (п6.2.1). Рассмотрим процесс решения системы (4.3) в предположении, что электропроводность аппроксимируется по узловым значениям s j , j=1,M .
Линеаризуем функционал Ф в окрестности исследуемой точки s 0 разложив его в ряд Тейлора с использованием только первых производных.
Пусть y = maxФ i ’ = Ф p ’ і 0. В этом случае мы можем свести задачу (4.4) к эквивалентной задаче линейного программирования, состоящей в условной минимизации функции y . Рассмотрим процесс приведения задачи линейного программирования к каноническому виду. Раскрывая модуль в (4.5) получаем систему уравнений
Рассмотрим выражение под модулем в (4.5) и введем некоторые обозначения
С учетом системы (4.8 - 4.10) постановка задачи (4.4) принимает вид
Раскрывая скобки в (4.11) и исключая y из первых 2N неравенств кроме р -го получаем систему неравенств
Приведем систему неравенств (4.12) к каноническому виду (6.1). Для этого, в соответствии со стандартным подходом, запишем все неравенства в виде равенств, добавляя в левые части неравенств неотрицательные переменные v .
В матричном виде полученная система имеет вид Ax = b (4.14), где искомый вектор-столбец из 2(N+M)+1 элементов имеет вид x = ( y , z 1 , ... , z M , v 1 , ... , v 2N+M ) T . В системе линейных алгебраических уравнений (4.13) параметр минимизации y определен строкой с номером p , которую в дальнейшем будем называть базовой. Рассмотрим алгоритм симплексного метода для решения задачи (4.14):
Решая систему (4.14) находим вектор s min , соответствующий текущему решению задачи(4.13). Возвращаясь к методу условного градиента отметим, что направление спуска определяется как -s n = s min - s 0 , а очередное итерационное решение задачи (4.3) определяется выражением s n+1 = s n - a Ч s n . Для получения окончательного результата требуется определить оптимальную величину шага a в направлении s n , что можно осуществить путем одномерной минимизации функции s ( a )= s n - a Ч s n методом золотого сечения. 5. Некорректные задачи 5.1 Основные понятия. Корректность по Адамару В самом общем виде большинство обратных задач может быть представлено в виде операторного уравнения
где А - оператор, определенный на непустом множестве некоторого метрического пространства Х с метрикой r X и действующий в метрическое пространство F с метрикой r F , а по заданному элементу f требуется определить решение х [10-14]. Введем в пространстве X норму || x ||= Ц е x i 2 и в пространстве F норму || f ||= Ц е f j 2 . Заметим, что метрики r в соответствующих пространствах будут иметь вид r (x,y)=\\x-y \\ . В нашем случае обозначения в (5.1) имеют следующий смысл:
Согласно классического определения задача (5.1) называется корректной по Адамару если при любой фиксированной правой части ее решение:
В реальных условиях правая часть (5.1) известна всегда с некоторой погрешностью, т.е. f = f0 + d f , причем обычно f0 принадлежит пространству гладких функций, а погрешность d f выводит ее из этого класса. Вследствие этого получаем постановку задачи, для решения которой невозможно применение обычных методов решения корректных задач, т.к. любой фиксированной правой части (5.1) соответствует бесконечное множество наборов исходных данных т.е. возможных распределений ЭП по глубине пластины. 5.2 Корректность по Тихонову Задача (5.1) называется корректной по Тихонову на множестве корректности М М X если:
В данном подходе к вопросу корректности существование решения и его принадлежность некоторому множеству не доказывается, а постулируется в самой постановке задачи. Физически гипотеза о принадлежности искомого решения определенному множеству корректности может интерпретироваться для нашей задачи предположениями:
5.3 Вариационные методы решения некорректных задач Вариационные методы решения некорректных задач являются наиболее универсальными из известных способов решения. Практически любая некорректная задача, для которой разработан какой-либо метод решения, может быть решена также и вариационным способом[15]. Для выбора подходящего метода решения обратной задачи рассмотрим постановки наиболее распространенных вариационных методов в терминах вычислительной математики и нашей задачи. Пусть фиксированный набор данных состоит из измеренных на N частотах N комплексных значений вносимой ЭДС Uiизм , текущее рассчитанное значение которых Ui( s ) . Требуется определить для выбранного типа аппроксимации ЭП значения М параметров аппроксимации ( обычно используются узловые значения ). 5.3.1 Метод регуляризации Метод основан на стабилизации невязки r (Ax,f) при помощи вспомогательного неотрицательного функционала W (x) . Идея метода состоит в том, чтобы минимизировать обладающий сглаживающими свойставами функционал Ф(x,f) , имеющий следующий вид:
Используя классический регуляризирующий функционал вида
Основное преимущество метода состоит в регуляризации простейшим способом, в рамках использования квадратичного функционала. Это позволяет использовать для решения некорректной задачи хорошо известные и легко программируемые методы минимизации квадратичных функционалов [17]. Оборотной стороной достоинств метода являются его недостатки. Требование минимизации нормы решения и, как следствие, выбор гладкой реализации, в нашем случае будет приходить в противоречие с физикой задачи и в принципе не позволит находить решения с выраженным приповерхностным изменением ЭП. Еще один принципиальный недостаток метода состоит в постановке функционала как квадратичного, единого для всех измерений. Его минимум в общем случае не гарантирует минимизацию отклонения для произвольного i -го измерения в следствии нелокальности условия минимизации. Кроме того, следует учитывать отсутствие надежных априорных рекомендаций по выбору параметра регуляризации a . Обычно подходящие значения a можно подобрать только после ряда численных экспериментов по решению однотипных задач. Изменение характера искомого решения приводит к необходимости поиска нового значения a . 5.3.2 Метод квазирешений Метод использует одну из форм критерия невязки и заключается в сведении невязки к минимуму на некотором непустом множестве P , содержащем подмножество искомых решений. Квазирешением уравнения (5.1) на множестве P М X называется всякий элемент y О P для которого справедливо равенство r F ( Ay , f ) = inf( Ax , f ), x О P . Понятие квазирешения обобщает понятие решения, а для его существования не требуется принадлежность решения множеству P . Исходя из вышеизложенного получаем постановку метода в виде задачи условной минимизации функционала Ф(x,f) :
Отметим, что множество Р может иметь простой вид, например интервала [ x min , x max ]. В терминах нашей задачи ВТК постановка задачи (5.4) примет вид:
Для того, чтобы гарантировать минимизацию отклонения для произвольного i -го измерения, можно применить к первому выражению в (5.5) локальный в смысле Чебышева критерий, в соответствии с которым получаем окончательное выражение :
Основное преимущество метода состоит в том, что само понятие квазирешения снимает трудности с требованиями тихоновской корректности: первым (вызывающим переопределенность задачи) и третьим (обычно принадлежность приближенной правой части уравнения (5.1) множеству N=AM неизвестна, а критерии этой принадлежности часто сами бывают неустойчивы). Кроме этого при рассмотрении задачи в виде (5.6) возможна постановка минимизационной задачи как задачи нелинейного программирования с явно заданными ограничениями на искомые переменные. В этом случае нет необходимости искажать исходный функционал регуляризующими членами как в (п5.3.1), а требования к искомому решению можно удовлетворить, управляя ограничениями на параметры минимизации (в нашем случае - узловые значения ЭП). 5.3.3 Метод невязки Рассмотрим множество Р формальных решений уравнения (5.1) Р={x : r F ( Ax , f d ) Ј d }, где f d - приближенная правая часть (5.1), известная с погрешностью d . В качестве приближенного решения (5.1) нельзя брать произвольный элемент множества Р , т.к. не гарантируется близость Р к множеству точных решений. Для выбора приближенного решения предлагается использовать стабилизирующий функционал W (х) из (п 5.3.1) следующим образом: W ( х ) = inf W ( х ), x О P . Этот способ приводит к выбору элементов множества Р имеющих минимально допустимую невязку. С учетом этого постановка метода состоит в условной минимизации функционала Ф(х) :
Как и для метода регуляризации можно использовать стабилизирующий функционал вида W (х)=||x|| 2 , что приводит в обозначениях нашей задачи к системе:
При использовании локального в смысле Чебышева критерия система (5.8) окончательно примет вид:
6. Нелинейное программирование Содержание нелинейного программирования составляют теория и методы решения задач о нахождении экстремумов нелинейных функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами)[16-29]. Рассмотрим наиболее распространенные методы решения на примере основной задачи нелинейного программирования вида:
6.1 Метод штрафных функций Идея метода состоит в замене экстремальной задачи с ограничениями (6.1) на задачу безусловной минимизации однопараметрической функции
Непрерывную функцию y (х) называют штрафом, если y (х)=0 для х О Х и y (х)>0 в противном случае. Функция y (х) должна быть выбрана таким образом, чтобы решение задачи (6.2) сходилось при b ® 0 к решению исходной задачи (6.1) или, по крайней мере, стремилось к нему. Приведем часто используемые выражения для штрафа :
Наибольшее применение находит штраф (6.3). Выражение (6.5) гарантирует конечность метода при любом k>0 . При численной реализации метода штрафных функций возникают проблемы выбора начального значения параметра b и способа его изменения. Сложность состоит в том, что выбор достаточно малого b увеличивает вероятность сходимости решения (6.2) к решению (6.1), а скорость сходимости градиентных методов вычисления точек минимума (6.2), как правило, падает с убыванием величины b . 6.2 Релаксационные методы Релаксационным методом называют процесс построения последовательности точек {х k : х k О X , j ( х k+1 ) Ј j ( х k ) ; k=0,1... }. Основными представителями этого класса являются методы спуска, алгоритм которых состоит из следующих шагов :
Различия методов состоят в выборе либо направления спуска, либо способа движения вдоль выбранного направления. В последнем случае обычно используют одномерную минимизацию функции х k+1 ( a ) = х k - a Ч s k (при этом точность вычисления точки минимума функции х k+1 ( a ) следует согласовывать с точностью вычисления значений функции j (х) ) или способ удвоения a (величина шага удваивается пока выполняется условие j (х k+1 ) Ј j (х k ) ). 6.2.1 Метод условного градиента Идея метода заключается в линеаризации нелинейной функции j (х). В этом методе выбор направления спуска осуществляется следующим образом :
Таким образом итерация метода имеет вид: x k+1 =x k + a k Ч (s k+1 - x k ) , s k+1 =arg min( С f(x k ),x). Основное преимущество метода проявляется в случае задания допустимого множества с помощью линейных ограничений. В этом случае получаем задачу линейного программирования, решаемую стандартными методами(например симплексным). 6.2.2 Метод проекции градиента Этот метод является аналогом метода градиентного спуска, используемого в задачах без ограничений. Его идея состоит в проектировании точек, найденных методом наискорейшего спуска, на допустимое множество, определяемое ограничениями. Проекцией точки y на множество Х называется точка P(y) О Х такая, что || P(y) - y || Ј || x - y || для всех х О Х. Задача проектирования формализуется как || x - y || 2 ® min, x О Х. Выбор направления спуска осуществляется следующим образом :
Таким образом итерация метода имеет вид: x k+1 =P X [ x k - a k Ч С f( x k ) ], где Р X (у) - ортогональная проекция точки у на множество Х . Для отыскания направления спуска s k необходимо решить задачу минимизации квадратичной функции || r k - х || 2 на множестве Х . В общем случае эта задача того же порядка сложности, что и исходная, однако для задач, допустимое множество которых имеет простую геометрическую структуру, отыскание проекции значительно упрщается. Например, для многомерного параллелепипида Q N ={x О R N : a Ј x Ј b }, отыскание проекции осуществляется путем сравнения n чисел и имеет вид P(x)={ a i , x i < a i ; x i , x i О [ a i ,b i ] ; b i , x i > b i }. 6.2.3 Метод случайного спуска Метод характеризуется тем, что в качестве направления спуска s K выбирается некоторая реализация n -мерной случайной величины S с известным законом распределения. Об эффективности этого метода судить трудно, однако благодаря использованию быстродействующих ЭВМ он оказывается практически полезным. 6.3 Метод множителей Лагранжа Идея метода состоит в отыскании седловой точки функции Лагранжа задачи (6.1). Для нахождения решения вводится набор переменных l i , называемых множители Лагранжа, и составляется функция Лагранжа, имеющая вид:
Алгоритм метода состоит в следующем:
Решениями системы (6.8) являются точки, которые могут быть решениями задачи.
7. Линейное программирование Задача линейного программирования в каноническом виде имеет вид[15,16]:
Приведение к каноническому виду любой задачи линейного программирования осуществляется путем введения дополнительных неотрицательных переменных, за счет чего ограничения, имеющие вид неравенств, принимают вид эквивалентных им равенств. Любая задача линейного программирования может быть решена за конечное число итераций с помощью симплексного метода[17,18]. Следует отметить, что поскольку этот метод разработан для неотрицательных элементов x j , это условие учитывается неявно и в систему уравнений (7.1) при численной реализации не входит. 7.1 Алгоритм симплексного метода 1. Приведение к каноническому виду 2. Выбор начального базиса 3. Проверка оптимальности базиса Матрицу А можно рассматривать как совокупность столбцов a j т.е. е a j Ч x j =b где j=1,N . Не ограничивая общности можно считать, что базис образуют первые m столбцов, тогда остальные можно представить в виде a k = е a j Ч l jk , j=1,m где l jk . - некоторые числа. Рассмотрим коэффициенты D k = е c j Ч l jk - c k где j=1,m и k=1,N . Заметим, что для базовых столбцов D k є 0 . Проверка на оптимальность осуществляется следующим образом:
4. Составление нового базиса 4.1 Выбор элемента для введения в базис. В базис вводится любой столбец, для которого D k < 0 , обозначим его D p 4.2 Выбор элемента исключаемого из базиса Из текущего базиса исключается столбец, для которого минимально отношение b i /A ip , i=1,M обозначим его b r /A rp
4.4 Переход к пункту 3
8. Одномерная минимизация Несмотря на кажущуюся простоту, для широкого класса функций решение задачи минимизация функции одного переменного j (х) сопряжено с некоторыми трудностями. С одной стороны, в практических задачах часто неизвестно, является ли функция дифференцируемой. С другой стороны, задача решения уравнения j ў (х)=0 может на практике оказаться весьма сложной. Ввиду этого существенное значение приобретают методы минимизации, не требующие вычисления производной[15]. Поскольку нас интересует приближенное определение точки минимума, то для этого исследуют поведение функции в конечном числе точек, способами выбора которых различаются методы одномерной минимизации. К методам, в которых при ограничениях на количество вычислений значений j (х) достигается в определенном смысле наилучшая точность, относятся методы Фибоначчи и золотого сечения[17,18]. Оба метода строятся по единой схеме и различаются способом выбора параметра l . Исходными данными для них являются: отрезок [a 0 ,b 0 ] содержащий точку минимума и точность определения точки минимума e . 8.1 Алгоритм методов
Следует отметить, что на каждом шаге кроме первого, производится только одно вычисление значения функции j (x) . Легко показать, что для получения оптимальной последовательности отрезков, стягивающихся к точке минимума, необходимо положить l k = F k-1 / F k , где F - число Фибоначчи. 8.2 Метод Фибоначчи Решая вопрос, при каких значениях параметра l за конечное число итераций N мы получим отрезок минимальной длины, получим l = l N = F N-1 / F N . Иначе говоря, для поиска минимума первоначально необходимо найти число Фибоначчи N такое, что F N+1 < (b 0 -a 0 )/ e Ј F N+2 . 8.3 Метод золотого сечения В реальной ситуации начиная поиск минимума мы не знаем точного числа требуемых итераций. Вместо вычисления l будем выдерживать постоянное отношение длин интервалов h k-2 /h k-1 = h k-1 /h k = t . При t = ( Ц 5+1)/2 = 1.618034 получаем метод золотого сечения. Сравнивая приведенные методы при больших значениях N можно показать, что значение окончательного интервала неопределенности в методе золотого сечения лишь на 17% больше чем в методе Фибоначчи.
9. Результаты численного моделирования 9.1 Аппроксимации при численном моделировании Для построения моделей реальных распределений ЭП возможно применение целого ряда аппроксимаций. Все они могут быть разделены на два класса. 1. Аппроксимации, строящиеся по набору из произвольного числа узлов. Наиболее распространенные из них: кусочно-постоянная, кусочно-линейная и сплайном. В условиях нашей задачи указанные аппроксимации имеют несколько существенных недостатков:
2. Аппроксимации, строящиеся по значениям ЭП на верхней и нижней поверхностях пластины и нескольким параметрам аппроксимации. Наиболее известные из них: экспоненциальная, гиперболическим тангенсом и гауссоидой. Аппроксимации имеют вид:
где
Для нашей задачи подобные аппроксимации являются предпочтительными, поскольку обладают заметными достоинствами:
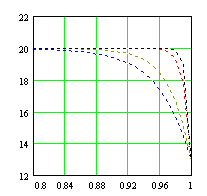
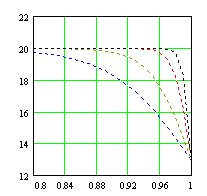
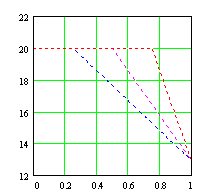
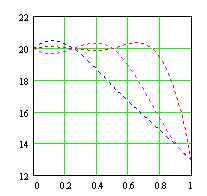
Для иллюстрации наших рассуждений приведем пример применения приведенных выше аппроксимаций к случаю восстановления кусочно-линейной функции. По оси абсцисс отложена относительная глубина, по оси ординат электропроводность (МСм/м).
9.2 Модели реальных распределений электропроводности Модель задачи должна описывать некоторую пластину, подвергнутую поверхностной обработке. Для определенности зададим толщину пластины равной двум сантиметрам. На основе данных из Приложения 2 зададим значения ЭП вблизи нижней и верхней поверхностей соответственно 20 (МСм/м) и 13 (МСм/м) . Для решения обратной задачи необходимо задать априорную информацию о величине ЭП в узлах аппроксимации. В качестве таковой примем интервал [8,25] (МСм/м) , полученный внесением 25% отклонения от считаемых истинными значений. Это отклонение моделирует неточность априорной информации. Из-за особенностей реализации алгоритма устойчивость решения сильно зависит от точности задания ЭП в узле, соответствующем нижней поверхности пластины, поэтому ограничение в нем зададим интервалом [19,21] (МСм/м) . В нашем случае все возможные модели распределений ЭП могут быть разделены на два класса. Распределения относящиеся к первому из них условно назовем глубинными. В них ЭП претерпевает существенные изменения на протяжении всей глубины пластины. Второй класс образуют распределения, ЭП в которых заметно изменяется лишь в приповерхностном слое глубиной порядка четверти пластины., поэтому назовем эти распределения поверхностными. Критерием отличия восстановленной функции распределения ЭП от модельной будем считать величину относительной погрешности, поскольку сравнение результатов с ее помощью вполне адекватно целям нашей работы. Следует отметит, что погрешность восстановления для поверхностных распределений ЭП представляет практический интерес в области, примерно ограниченной глубиной порядка четверти пластины, что обусловлено физическим смыслом поверхностной обработки. Поэтому для случаев поверхностных распределений основное внимание будем уделят именно указанным глубинам. Для проверки возможности восстановления приповерхностных изменений ЭП рассмотрим две базовые модели поверхностных распределений.
Для проверки возможности восстановления глубинных распределений ЭП рассмотрим две базовые модели глубинных распределений.
Заметим, что на практике можно осуществить достаточно точное определение величины ЭП приповерхностных слоев путем измерений проводимости традиционными средствами, поэтому дополнительно рассмотрим модельные задачи при условии известной ЭП на верхней, а так же верхней и нижней поверхностях. Поскольку на практике результаты измерений вносимого напряжения имеют определенную погрешность, все модели будем рассчитывать эмулируя погрешность d U= 0,1,2,5% . Для исследования зависимости результатов восстановления распределений ЭП от частоты возбуждения разобьем частотный диапазона три части следующим образом( глубины проникновения приведены для случая постоянной ЭП s =13 МСм/м ):
Для исследования зависимости результатов восстановления распределений ЭП от числа измеряемых вносимых напряжений N рассмотрим случаи N={ 5, 10, 15 } . Низкие частоты
Средние частоты
Высокие частоты
9.3 Принципиальная возможность восстановления Для исследования возможности восстановления распределения ЭП рассмотрим результаты, полученные в предположении наличия точных данных (погрешность измерения отсутствует). На графиках в первых четырех пунктах Приложения 3 рассматриваемые зависимости показаны красным цветом (исходные данные черным). Исходя из них можно сделать следующие выводы
9.4 Восстановление по зашумленным данным Рассмотренные в данном разделе результаты демонстрируют возможность восстановления распределений ЭП в реальных условиях. Графики представлены в первых четырех пунктах Приложения 3 . На графиках рассматриваемые зависимости показаны цветами: результат восстановления при погрешности данных равной 1% - голубым, результат восстановления при погрешности данных равной 2% - коричневым, результат восстановления при погрешности данных равной 5% - синим. Исходя из них можно сделать следующие выводы:
9.5 Восстановление с учетом дополнительной информации С целью улучшения результатов восстановления в реальной обстановке, осложненной наличием зашумленных данных, следует использовать более жесткие ограничения на величину ЭП в приповерхностных слоях. Для иллюстрации приведем несколько графиков, представленных в пятом пункте Приложения 3 . На графиках рассматриваемые зависимости показаны цветами: базовые ограничения - коричневым, жесткие ограничения на верхней поверхности - голубым, жесткие ограничения на обоих поверхностях - малиновым. Исходя из полученных результатов можно сделать следующие выводы
9.6 Восстановление при различном возбуждении Для выбора необходимого количества измерений U вн * и соответствующих им частот возбуждения ВТП рассмотрим три возможных диапазона частот, в каждом из которых исследуем случаи пяти, десяти и пятнадцати частот. На графиках в шестом пункте Приложения 3 рассматриваемые зависимости показаны цветами: 5 частот - коричневым, 10 частот - голубым , 15 частот - малиновым. Область низких частот Исходя из полученных результатов можно сделать следующие выводы
Область средних частот Исходя из полученных результатов можно сделать следующие выводы:
Область высоких частот Исходя из полученных результатов можно сделать следующие выводы:
10. Заключение По результатам проделанной работы можно сделать следующие выводы:
В процессе работы над задачей был проведен анализ литературы, выбрана модель задачи и способы ее аппроксимации. При помощи программы, разработанной согласно предложенной модели, были проведены расчеты модельных задач и рассмотрены результаты восстановления распределений ЭП в зависимости от основных влияющих факторов. Таким образом, цели, поставленные в техническом задании, решены в полном объеме. 11. Литература
Приложение 1. Программная реализация Программная реализация изложенного метода решения обратной задачи ВТК осуществлена при помощи компилятора Borland Pascal 7.0 и состоит из шести модулей:
П1.1 Исходные данные Исходные данные программы хранятся в текстовом файле( кодировка ASCII, расширение по умолчанию TXT ).
П1.2 Используемые аппроксимации Примечание. Координата Х О [0,1] отсчитывается от дна пластины для всех аппроксимаций. Сплайн(SPL), кусочно-линейная(PWL), кусочно-постоянная(PWC) аппроксимации. В процессе расчетов ищутся значения электропроводности в узлах аппроксимации, причем количество узлов увеличивается от едениицы до nPoints в целях сохранения устойчивости решения. Начальные значения (узловые значения І истинной І ЭП для эмуляции измерений U * вн ) задаются в столбце І si І файла исходных данных, начальные значения ограничений на узловые значения ЭП в столбцах І siMin І и І siMax І (движение по столбцу сверху вниз соответствует изменению координаты от дна пластины до обрабатываемой повехности). Экспоненциальная аппроксимация(EXP) В случае задания экспоненциальной аппроксимации зависимость электропрводности от толщины представляется в виде SIGMA = ( siE-siI )*EXP( -alfa*(1-x) ) + siI Варьруемыми параметрами являются эектропроводность на верхней поверхности siЕ , электропроводность "на бесконечности" siI и параметр alfa . В файле исходных данных в таблице из nPoints строк с подзаголовком "si siMin siMax", информация об ограничениях на параметры siE, siI задается в первой и nPoints -строке. Величина и ограничения для параметра alfa задаются первой строкой в "special approximation parameters". Аппроксимация гиперболическим тангенсом (HTG) В случае задания аппроксимации гиперболическим тангенсом зависимость электропрводности от толщины представляется в виде SIGMA = si2 + ( si1-si2 )/2*{ 1 + th( ( beta-x )/gamma ) } Величина и ограничения для параметров si2,beta,gamma задаются начиная со второй строки в "special approximation parameters", для si1 аналогично siI. П1.3 Результаты расчета Результаты расчета помещаются в текстовый файл( кодировка ASCII, расширение по умолчанию LST ), при этом результат каждой итерации отбражается строкой вида: 1 <Ф> 0.000353 Rg= 17.003 15.639 9.697 где первая цифра (в данном случае 1) соответствует номеру текущей внутренней итерации, затем после текста "<Ф>" идет значение текущей абсолютной среднеквадратичной невязки по всем гармоникам (в данном случае 0.000353), затем после текста "Rg= ", идут искомые текущие значения переменных минимизации. В случае SPL,PWL,PWC аппроксимаций это непосредственно узловые значения электропроводности для текущего количества узлов, а для EXP,HTG аппроксимаций это параметры { siE, siI, Alfa } или { si1, si2, Beta, Gamma }. B качестве последней строки помещаются nPoints вычисленных значений э/проводности в равномерно расположенных узлах пластины.
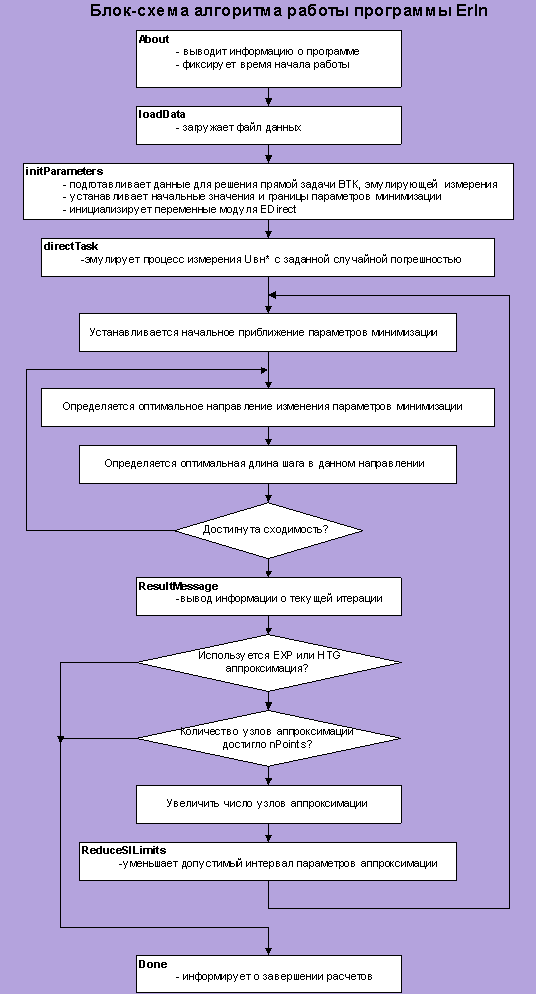
П1.4 Основная программа ErIn (****************************************************************************) (* ErIn v1.42 *) (* Eddy current inverse problem solver. *) (* (C) 1999 by Nikita U.Dolgov *) (* Moscow Power Engineering Institute , Introscopy dept. *) {****************************************************************************} Program ErIn;{23.02.99} Uses DOS,CRT, EData, EMath, EDirect, EFile, EMinimum; Var m, mLast, i : byte; {loop counters} procedure about; {Let me to introduce myself} begin clrscr; GetTime( clk1.H, clk1.M, clk1.S, clk1.S100 ); {get start time} writeln('***********************************************************'); writeln('* ErIn v1.42 Basic * *'); writeln('***********************************************************'); end; procedure initParameters; var apDT : byte; {approximation type for direct task} begin apDT := nApprox SHR 4; {XXXXYYYY->0000XXXX} fHypTg:=(( apDT AND apHypTg ) = apHypTg); if fHypTg then begin si0[ 1 ]:=si[ 1 ]; {si1 - conductivity about bottom of slab} si0[ 2 ]:=par0[ 2 ]; {si2 - conductivity about top of slab} si0[ 3 ]:=par0[ 3 ]; {Beta - ratio of approx.} si0[ 4 ]:=par0[ 4 ]; {Gamma- ratio of approx.} mCur:=4; end else if(( apDT AND apExp ) = 0 ) then {It's not an EXP approx.} begin for i:=1 to nPoints do si0[ i ] :=si [ i ]; {SI data from file} mCur:=nPoints; end else begin si0[ 1 ]:=si[ 1 ]; {siI - conductivity about bottom of slab} si0[ 2 ]:=si[ nPoints ]; {siE - conductivity about top of slab} si0[ 3 ]:=par0[ 1 ]; {Alfa- ratio of approx.} mCur:=3; end; setApproximationType( apDT ); {approx. type for direct problem} setApproximationData( si0, mCur ); {approx. data for direct problem} nApprox := ( nApprox AND $0F ); {XXXXYYYY->0000YYYY} fHypTg := (( nApprox AND apHypTg ) = apHypTg ); fMulti := (( nApprox AND apExp ) = 0 ) AND NOT fHypTg; {It's not an EXP approx.} if fMulti then begin for i:=1 to nPoints do begin Gr[ 1,i ]:=SiMax[ i ]; Gr[ 2,i ]:=SiMin[ i ]; Rg[ i ]:=( Gr[ 1,i ] + Gr[ 2,i ] )/2; {zero estimate of SI} Rgs[ i ]:=1E33; {biggest integer} end; mLast:=nPoints; {loop for every node of approx.} mCur :=1; {to begin from the only node of approx} end else if fHypTg then begin Gr[ 1,1 ]:= siMax[ 1 ]; Gr[ 2,1 ]:= siMin[ 1 ]; Rgs[ 1 ]:=1E33; Gr[ 1,2 ]:=parMax[ 2 ]; Gr[ 2,2 ]:=parMin[ 2 ]; Rgs[ 2 ]:=1E33; Gr[ 1,3 ]:=parMax[ 3 ]; Gr[ 2,3 ]:=parMin[ 3 ]; Rgs[ 3 ]:=1E33; Gr[ 1,4 ]:=parMax[ 4 ]; Gr[ 2,4 ]:=parMin[ 4 ]; Rgs[ 4 ]:=1E33; for i:=1 to 4 do Rg[ i ]:=( Gr[ 1,i ] + Gr[ 2,i ] )/2; mLast:=1; mCur:=4; end else begin Gr[ 1,1 ]:= siMax[1]; Gr[2,1]:= siMin[1]; Rgs[ 1 ]:=1E33; Gr[ 1,2 ]:= siMax[nPoints]; Gr[2,2]:= siMin[nPoints]; Rgs[ 2 ]:=1E33; Gr[ 1,3 ]:= parMax[1]; Gr[2,3]:= parMin[1]; Rgs[ 3 ]:=1E33; for i:=1 to 3 do Rg[ i ]:=( Gr[ 1,i ] + Gr[ 2,i ] )/2; mLast:=1; mCur :=3; end; initConst( nLayers, parMaxH, parMaxX , parEps, parEqlB );{set probe params} end; procedure directTask; {emulate voltage measurements [with error]} begin for i:=1 to nFreqs do begin getVoltage( freqs[i], Umr[ i ], Umi[ i ] ); {"measured" Uvn*} if ( epsU > 0 ) then {add measurement error} begin randomize; Umr[ i ]:=Umr[ i ]*( 1 + epsU*( random-0.5 ) ); randomize; Umi[ i ]:=Umi[ i ]*( 1 + epsU*( random-0.5 ) ); end; end; writeln('* Voltage measurements have been emulated'); setApproximationType( nApprox ); {approx. type for inverse problem} setApproximationData( Rg, mCur ); {approx. data for inverse problem} end; procedure reduceSILimits; {evaluate SI for m+1 points of approx. using aG} var x0, x1, xL, dx, Gr1, Gr2 : real; j, k : byte; begin {----------------------------- get SI min/max for m+1 points of approximation} dx:=1/( nPoints-1 ); for i:=1 to m+1 do begin k:=1; x1:=0; x0:=( i-1 )/m; for j:=1 to nPoints-1 do begin xL:=( j-1 )/( nPoints-1 ); if( ( xL < x0 ) AND ( x0 <= xL+dx ) )then begin k:=j; x1:=xL; end; end; Gr[ 1,i ]:=siMax[ k ] + ( siMax[ k+1 ]-siMax[ k ] )*( x0-x1 )/dx; Gr[ 2,i ]:=siMin[ k ] + ( siMin[ k+1 ]-siMin[ k ] )*( x0-x1 )/dx; end; {------------------------------------- get SI for m+1 points of approximation} for i:=1 to m+1 do begin Rg[i]:=getSiFunction( (i-1)/m ); if ( Rg[i] > Gr[1,i] )then Rg[i]:=Gr[1,i]; if ( Rg[i] < Gr[2,i] )then Rg[i]:=Gr[2,i]; if m > 1 then {There're more than 1 point of approx.} begin Gr1:= Rg[i]+( Gr[1,i]-Rg[i] )*aG; {reduce upper bound} Gr2:= Rg[i]-( Rg[i]-Gr[2,i] )*aG; {reduce lower bound} if ( Gr1 < Gr[1,i] )then Gr[1,i]:=Gr1; {test overflow} if ( Gr2 > Gr[2,i] )then Gr[2,i]:=Gr2; end; end; setApproximationData( Rg , m+1 ); end; procedure resultMessage; {to announce new results} begin if fMulti then begin writeln(' current nodal values of conductivity'); write(' si : ');for i:=1 to m do write(Rg[i] :6:3,' ');writeln; write(' max: ');for i:=1 to m do write(Gr[1,i]:6:3,' ');writeln; write(' min: ');for i:=1 to m do write(Gr[2,i]:6:3,' ');writeln; end else begin for i:=1 to nPoints do si[i]:=getSiFunction( ( i-1 )/( nPoints-1 ) ); if fHypTg then saveHypTgResults else saveExpResults; end; end; procedure clockMessage; {user-friendly message} begin writeln('***********************************************************'); write( '* approximation points number :',m:3,' * Time '); clock; writeln('***********************************************************'); end; procedure done; {final message} begin Sound(222); Delay(111); Sound(444); Delay(111); NoSound; {beep} write('* Task processing time '); clock; saveTime; writeln('* Status: Inverse problem has been successfully evaluated.'); end; Begin about; loadData; initParameters; directTask; for m:=1 to mLast do begin if fMulti then begin mCur:=m; clockMessage; end; doMinimization; {main part of work} setApproximationData( Rg, mCur ); {set new approx. data} resultMessage; if(( fMulti )AND( m < nPoints ))then reduceSILimits; end; done; End. П1.5 Модуль глобальных данных EData Unit EData; Interface Uses DOS; Const maxPAR = 40; {nodes of approximation max number} maxFUN = 20; {excitation frequencies max number} maxSPC = 4; {support approximation values number} iterImax = 50; {max number of internal iterations} Const apSpline = 1; {approximation type identifiers} apHypTg = 3; apExp = 2; apPWCon = 4; apPWLin = 8; Type Parameters = array[ 1..maxPAR ] of real; {Si,Mu data} Functionals = array[ 1..maxFUN ] of real; {Voltage data} SpecialPar = array[ 1..maxSPC ] of real; {Special data} Var hThick : real; {thickness of slab} nPoints : integer; {nodes of approximation number within [ 0,H ]} nLayers : integer; {number of piecewise constant SI layers within[ 0,H ]} nFreqs : integer; {number of excitation frequencies} nStab : integer; {required number of true digits in SI estimation} epsU : real; {relative error of measurement Uvn*} nApprox : byte; {approximation type identifier} incVal : real; {step for numerical differ.} parMaxH : integer; {max number of integration steps} parMaxX : real; {upper bound of integration} parEps : real; {error of integration} derivType: byte; {1 for right; 2 for central} Var freqs : Functionals; {frequencies of excitment Uvn*} Umr, Umi : Functionals; { Re(Uvn*),Im(Uvn*) for "measured" data} Uer, Uei : Functionals; { Re(Uvn*),Im(Uvn*) for estimated data} mu : Parameters; {relative permeability nodal values} si, si0 : Parameters; {conductivity approximation nodal values} siMin, siMax : Parameters; {conductivity nodal values restrictions} par0 : SpecialPar; {alfa,si2,beta,gamma - for exp&HypTg} parMin,parMax: SpecialPar; {-||- min/max} zLayer : Parameters; {relative borders of slab layers [0,1]} Var aG : real; {scale factor for SImin/max} Ft : real; {current discrepancy functional value} fMulti : boolean; {TRUE if it isn't an EXP-approximation} fHypTg : boolean; {TRUE for Hyperbolic tg approximation} parEqlB : boolean; {TRUE if b[i]=const} mCur : integer; {current number of approximation nodes} inFileName : string; {data file name} outFileName : string; {results file name} Var Rg : Parameters; {current SI estimation} RgS : Parameters; {previous SI estimation} Gr : array [ 1..2 ,1..maxPAR ] of real; {SI max/min} Fh : array [ 1..maxPAR , 1..maxFUN ] of real; {current discrepancies} Type TTime=record H, M, S, S100 : word; {hour,min,sec,sec/100} end; Var clk1, clk2 : TTime; {start&finish time} procedure loadData; {load all user-defined data from file} Implementation procedure loadData; var i,eqlB : integer; FF : text; begin assign( FF, outFileName ); {clear output file} rewrite( FF ); close( FF ); assign( FF, inFileName ); {read input file} reset( FF ); readln( FF ); readln( FF ); readln( FF, hThick, nPoints, nLayers, nFreqs, nStab, epsU, aG, nApprox ); readln( FF ); for i:=1 to nFreqs do read( FF, freqs[i] ); readln( FF ); readln( FF ); readln( FF ); for i:=1 to nPoints do readln( FF, si[i], siMin[i], siMax[i] ); readln( FF ); readln( FF ); readln( FF , incVal, parMaxH, parMaxX, parEps, derivType, eqlB ); readln( FF ); readln( FF ); for i:=1 to maxSPC do readln( FF, par0[i] , parMin[i] , parMax[i] ); readln( FF ); if ( eqlB=0 )then begin for i:=1 to nLayers+1 do read( FF, zLayer[i] ); parEqlB:=false; end else parEqlB:=true; close( FF ); for i:=1 to maxPAR do mu[i]:=1; end; Var str : string; Begin if( ParamCount = 1 )then str:=ParamStr(1) else begin write('Enter I/O file name, please: '); readln( str ); end; inFileName :=str+'.txt'; outFileName:=str+'.lst'; End. П1.6 Модуль работы с файлами EFile Unit EFile; Interface Uses DOS, EData; function isStable( ns : integer; var RG1,RG2 ) : boolean; function saveResults( ns,iter : integer ) : boolean; procedure saveExpResults; procedure saveHypTgResults; procedure clock; procedure saveTime; Implementation Var FF : text; i : byte; function decimalDegree( n:integer ) : real;{10^n} var s:real; i:byte; begin s:=1; for i:=1 to n do s:=s*10; decimalDegree:=s; end; function isStable( ns:integer ; var RG1,RG2 ) : boolean; var m : real; R1 : Parameters absolute RG1; R2 : Parameters absolute RG2; begin isStable:=TRUE; m:=decimalDegree( ns-1 ); for i:=1 to mCur do begin if NOT(( ABS( R2[i]-R1[i] )*m )<=ABS( R2[i]) ) then isStable:=FALSE; RgS[i]:=Rg[i]; end; end; function saveResults( ns , iter : integer ) : boolean; var sum : real; begin sum:=0; for i:=1 to nFreqs do sum:=sum + Fh[1,i]; sum:=SQRT( sum/nFreqs ); assign( FF , outFileName ); append( FF ); write( iter:2, ' <”>', sum:10:7, ' Rg=' ); write( FF , iter:2, ' <”>', sum:10:7, ' Rg='); for i:=1 to mCur do begin write( Rg[i]:6:3, ' '); write( FF , Rg[i]:6:3, ' '); end; writeln; writeln( FF ); close( FF ); saveResults:=isStable( ns , Rgs , Rg ); end; procedure saveExpResults; begin assign( FF , outFileName ); append( FF ); writeln( ' siE=',Rg[2]:6:3,' siI=',Rg[1]:6:3,' alfa=',Rg[3]:6:3); writeln( FF , ' siE=',Rg[2]:6:3,' siI=',Rg[1]:6:3,' alfa=',Rg[3]:6:3); write( ' SI: '); write( FF , ' SI: '); for i:=1 to nPoints do begin write( si[i]:6:3,' '); write( FF , si[i]:6:3,' '); end; writeln; writeln( FF ); close( FF ); end; procedure saveHypTgResults; begin assign( FF , outFileName ); append( FF ); writeln( ' si1=',Rg[2]:6:3,' si2=',Rg[1]:6:3,' beta=',Rg[3]:6:3,' gamma=',Rg[4]:6:3); writeln( FF , ' si1=',Rg[2]:6:3,' si2=',Rg[1]:6:3,' beta=',Rg[3]:6:3,' gamma=',Rg[4]:6:3); write( ' SI: '); write( FF , ' SI: '); for i:=1 to nPoints do begin write( si[i]:6:3,' '); write( FF , si[i]:6:3,' '); end; writeln; writeln( FF ); close( FF ); end; procedure clock; {t2 = t2-t1} var H1,M1,S1,H2,M2,S2,sec1,sec2 : longint; begin GetTime( clk2.H, clk2.M, clk2.S, clk2.S100 ); {current time} H2:=clk2.H; M2:=clk2.M; S2:=clk2.S; H1:=clk1.H; M1:=clk1.M; S1:=clk1.S; sec2:= ( H2*60 + M2 )*60 + S2; sec1:= ( H1*60 + M1 )*60 + S1; if( sec2 < sec1 )then sec2:=sec2 + 85020; {+23.59.59} sec2:=sec2 - sec1; clk2.H := sec2 div 3600; sec2:=sec2 - clk2.H*3600; clk2.M := sec2 div 60; sec2:=sec2 - clk2.M*60; clk2.S := sec2; writeln( clk2.H:2, ':', clk2.M:2, ':', clk2.S:2 ); end; procedure saveTime; begin assign( FF , outFileName ); append( FF ); write( FF ,'* Processing time ',clk2.H:2, ':', clk2.M:2, ':', clk2.S:2 ); close( FF ); end; End. П1.7 Модуль решения прямой задачи ВТК для НВТП EDirect {****************************************************************************} { ERIN submodule : EDirect , 15.02.99, (C) 1999 by Nikita U.Dolgov } {****************************************************************************} { Estimates Uvn* for Eddy current testing of inhomogeneous multilayer slab } { with surface( flat ) probe. } { It can do it using one of five types of conductivity approximation : } {Spline, Exponential, Piecewise constant, Piecewise linear,Hyperbolic tangent} {****************************************************************************} {$F+} Unit EDirect; Interface Uses EData, EMath; Type siFunc = function( x:real ) : real; Var getSiFunction : siFunc; {for external getting SI estimate} procedure initConst( par1,par2:integer; par3,par4:real; par5:boolean ); procedure getVoltage( freq : real ; var ur,ui : real ); { Uvn* = ur + j*ui } procedure setApproximationType( approx : byte ); { type of approx. } procedure setApproximationItem( SIG:real ; N : byte ); { set SIGMA[ N ]} procedure setApproximationData( var SIG; nVal : byte ); { SIGMA[1..nVal] } procedure getApproximationData( var SIG ; var N : byte ); { get SIGMA[ N ]} Implementation Const PI23 = 2000*pi; {2*pi*KHz} mu0 = 4*pi*1E-7; {magnetic const} Var appSigma : Parameters; {conductivity approximation data buffer} appCount : byte; {size of conductivity approximation data buffer} appType : byte; {conductivity approximation type identifier} Type commonInfo=record w : real; {cyclical excitation frecuency} R : real; {equivalent radius of probe} H : real; {generalized lift-off of probe} Kr : real; {parameter of probe} eps : real; {error of integration} xMax : real; {upper bound of integration} steps : integer; {current number of integration steps} maxsteps: integer; {max number of integration steps} Nlay : integer; {number of layers in slab} sigma : Parameters; {conductivity of layers} m : Parameters; {relative permeability of layers} b : Parameters; {thickness of layers} zCentre : Parameters; {centre of layer} end; procFunc = procedure( x:real; var result:complex); Var siB, siC, siD : Parameters; {support for Spline approx.} cInfo : commonInfo; {one-way access low level info} function siSpline( x:real ) : real;{Spline approximation} begin if( appCount = 1 )then siSpline := appSigma[ 1 ] else siSpline:=Seval( appCount, x, appSigma, siB, siC, siD); end; function siExp( x:real ) : real;{Exponential approximation} begin siExp:=(appSigma[2]-appSigma[1])*EXP( -appSigma[3]*(1-x) ) + appSigma[1]; end; function siPWConst( x:real ) : real;{Piecewise constant approximation} var dx, dh : real; i : byte; begin if( appCount = 1 )then siPWConst := appSigma[ 1 ] else begin dh:=1/( appCount-1 ); dx:=dh/2; i:=1; while( x > dx ) do begin i:=i + 1; dx:=dx + dh; end; siPWConst:=appSigma[ i ]; end; end; function siPWLinear( x:real ) : real;{Piecewise linear approximation} var dx, dh : real; i : byte; begin if( appCount = 1 )then siPWLinear := appSigma[ 1 ] else begin dh:=1/( appCount-1 ); dx:=0; i:=1; repeat i:=i + 1; dx:=dx + dh; until( x <= dx ); siPWLinear:=appSigma[i-1]+( appSigma[i]-appSigma[i-1] )*( x/dh+2-i); end; end; function siHyperTg( x:real ) : real;{Hyperbolic tangent approximation} begin siHyperTg:=appSigma[2]+(appSigma[1]-appSigma[2])*(1+th((appSigma[3]-x)/appSigma[4]))/2; end; procedure setApproximationType( approx : byte ); begin appType := approx; write('* conductivity approximation type : '); case approx of apSpline : begin writeln('SPLINE'); getSiFunction := siSpline; end; apExp : begin writeln('EXP'); getSiFunction := siExp; end; apPWCon : begin writeln('PIECEWISE CONST'); getSiFunction := siPWConst; end; apPWLin : begin writeln('PIECEWISE LINEAR'); getSiFunction := siPWLinear; end; apHypTg : begin writeln('HYPERBOLIC TANGENT'); getSiFunction := siHyperTg; end; end; end; procedure setApproximationData( var SIG ; nVal : byte ); var Sigma : Parameters absolute SIG; i:byte; begin appCount := nVal; for i:=1 to nVal do appSigma[ i ]:=Sigma[ i ]; if( appType = apSpline )then Spline( appCount, appSigma, siB, siC, siD); end; procedure getApproximationData( var SIG ; var N : byte ); var Sigma : Parameters absolute SIG; i:byte; begin N := appCount; for i:=1 to appCount do Sigma[ i ]:=appSigma[ i ]; end; procedure setApproximationItem( SIG:real ; N : byte ); begin appSigma[ N ] := SIG; if( appType = apSpline )then Spline( appCount, appSigma, siB, siC, siD); end; procedure functionFi( x:real ; var result:complex );{get boundary conditions function value} var beta : array[ 1..maxPAR ]of real; q : array[ 1..maxPAR ]of complex; fi : array[ 0..maxPAR ]of complex; th , z1 , z2 , z3 , z4 , z5 , z6 , z7 : complex; i : byte; begin mkComp( 0, 0, fi[0] ); with cInfo do for i:=1 to Nlay do begin beta[i]:=R*sqrt( w*mu0*sigma[i] ); {calculation of beta} mkComp( sqr(x), sqr(beta[i])*m[i], z7 ); {calculation of q, z7=q^2} SqrtC( z7, q[i] ); mulComp( q[i], b[i], z6 ); {calculation of th,z6=q*b} tanH( z6, th ); {th=tanH(q*b)} mkComp( sqr(m[i])*sqr(x), 0, z6 ); {z6=m2x2} SubC( z6, z7, z5); {z5=m2x2-q2} AddC( z6, z7, z4); {z4=m2x2+q2} MulC( z5, th, z1); {z1=z5*th} MulC( z4, th, z2); {z2=z4*th} mulComp( q[i], 2*x*m[i], z3 ); {z3=2xmq} SubC( z2, z3, z4 ); MulC( z4, fi[i-1], z5 ); SubC( z1, z5, z6 ); {z6=high} AddC( z2, z3, z4 ); MulC( z1, fi[i-1], z5 ); SubC( z4, z5, th ); {th=low} DivC( z6, th, fi[i] ); end; eqlComp( result, fi[ cInfo.Nlay ] ); end; procedure funcSimple( x:real; var result:complex );{intergrand function value} var z : complex; begin with cInfo do begin functionFi( x, result ); mulComp( result, exp( -x*H ), z ); mulComp( z, J1( x*Kr ), result ); mulComp( result, J1( x/Kr ), z ); eqlComp( result, z ); end; end; procedure funcMax( x:real; var result:complex );{max value; When Fi[Nlay]=1} var z1, z2 : complex; begin with cInfo do begin mkComp( 1,0,z1 ); mulComp( z1, exp(-x*H), z2 ); mulComp( z2, J1( x*Kr ), z1 ); mulComp( z1, J1( x/Kr ), result ); end; end; procedure integralBS( func:procFunc ; var result:complex );{integral by Simpson} var z , y , tmp : complex; hh : real; i, iLast : word; begin with cInfo do begin hh:=xMax/steps; iLast:=steps div 2; nullComp(tmp); func( 0, z ); eqlComp( y, z ); for i:=1 to iLast do begin func( ( 2*i-1 )*hh , z ); deltaComp( tmp, z ); end; mulComp( tmp, 4, z ); deltaComp( y, z ); nullComp( tmp ); iLast:=iLast-1; for i:=1 to iLast do begin func( 2*i*hh ,z ); deltaComp( tmp, z ); end; mulComp( tmp, 2, z ); deltaComp( y, z ); func( xmax, z ); deltaComp(y,z); mulComp( y, hh/3, z ); eqlComp( result, z ); end; end;{I = h/3 * [ F0 + 4*sum(F2k-1) + 2*sum(F2k) + Fn ]} procedure integral( F:procFunc; var result:complex );{integral with given error} var e , e15 : real; flag : boolean; delta , integ1H , integ2H : complex; begin with cInfo do begin e15 :=eps*15;{ | I2h-I1h |/(2^k -1 )< Eps ; k=4 for Simpson method} steps:=20; flag :=false; integralBS( F, integ2H ); repeat eqlComp( integ1H, integ2H ); steps:=steps*2; integralBS( F, integ2H ); SubC( integ2H, integ1H, delta ); e:=Leng( delta ); if( e<e15 )then flag:=true; until( ( flag ) OR (steps>maxsteps) ); if( flag )then begin eqlComp( result, integ2H ); end else begin writeln('Error: Too big number of integration steps.'); halt(1); end; end; end; procedure initConst( par1, par2 : integer; par3, par4 : real; par5:boolean ); var i : byte; bThick, dl, x : real; const Ri=0.02; hi=0.005; { radius and lift-off of excitation coil} Rm=0.02; hm=0.005; { radius and lift-off of measuring coil} begin with cInfo do begin Nlay :=par1; xMax :=par3; maxsteps:=par2; R :=sqrt( Ri*Rm ); H :=( hi+hm )/R; Kr :=sqrt( Ri/Rm ); eps :=par4; bThick :=hThick*0.002/R; {2*b/R [m]} for i:=1 to Nlay do m[i]:= mu[i]; if par5 then begin bThick:=bThick/NLay; for i:=1 to Nlay do b[i]:=bThick; dl:=1/NLay; x:=dl/2; {x grows up from bottom of slab to the top} for i:=1 to Nlay do begin zCentre[i]:=x; x:=x + dl; end; end else for i:=1 to Nlay do begin b[i]:=( zLayer[i+1]-zLayer[i] )*bThick; zCentre[i]:=( zLayer[i+1]+zLayer[i] )/2; end; end; end; procedure init( f:real );{get current approach of conductivity values} var i : byte; begin with cInfo do begin w:=PI23*f; for i:=1 to Nlay do sigma[i]:=getSiFunction( zCentre[i] )*1E6; end; end; procedure getVoltage( freq : real ; var ur,ui : real ); var U, U0, Uvn, tmp : complex; begin init( freq ); integral( funcSimple, U ); { U =Uvn } integral( funcMax , U0 ); { U0=Uvn max } divComp( U, Leng(U0), Uvn ); { Uvn=U/|U0| } mkComp( 0, 1, tmp ); { tmp=( 0+j1 ) } MulC( tmp, Uvn, U ); { U= j*Uvn = Uvn* } ur := U.re; ui := U.im; end; END. П1.8 Модуль решения обратной задачи ВТК для НВТП EMinimum Unit EMinimum; INTERFACE Uses EData, Crt, EFile, EDirect; procedure doMinimization; IMPLEMENTATION procedure getFunctional( Reg : byte ); var ur, ui, dur, dui, Rgt : real; ur2, ui2: Functionals; i, j, k : byte; begin getApproximationData( si , k ); setApproximationData( Rg, mCur ); case Reg of 0 : for i:=1 to nFreqs do {get functional F value} begin getVoltage( freqs[i], ur, ui ); Uer[ i ]:=ur; {we need it for dU} Uei[ i ]:=ui; Fh[1,i] := SQR( ur-Umr[i] ) + SQR( ui-Umi[i] ); end; {Right:U'(i)= (U(i+1)-U(i))/h} 1 : for i:=1 to mCur do {get dF/dSI[i] value} begin Rgt:=Rg[i]*( 1+incVal ); {si[i]=si[i]+dsi[i]} setApproximationItem( Rgt, i ); {set new si[i] value} for j:=1 to nFreqs do begin {get dUr/dSI,dUi/dSI} getVoltage( freqs[ j ], ur, ui ); dur:=( ur-Uer[j] )/( Rg[i]*incVal ); dui:=( ui-Uei[j] )/( Rg[i]*incVal ); Fh[i,j]:=2*(dur*(Uer[j]-Umr[j])+dui*(Uei[j]-Umi[j])); end; setApproximationItem( Rg[i], i ); {restore si[i] value} end; {Central:U'(i)= (U(i+1)-U(i-1))/2h} 2 : for i:=1 to mCur do {get dF/dSI[i] value} begin Rgt:=Rg[i]*( 1+incVal ); {si[i]=si[i]+dsi[i]} setApproximationItem( Rgt, i ); {set new si[i] value} for j:=1 to nFreqs do getVoltage( freqs[j],ur2[j],ui2[j] ); Rgt:=Rg[i]*( 1-incVal ); {si[i]=si[i]-dsi[i]} setApproximationItem( Rgt, i ); {set new si[i] value} for j:=1 to nFreqs do begin {get dUr/dSI,dUi/dSI} getVoltage( freqs[ j ], ur, ui ); dur:=( ur2[j]-ur )/( 2*Rg[i]*incVal ); dui:=( ui2[j]-ui )/( 2*Rg[i]*incVal ); Fh[i,j]:=2*(dur*(Uer[j]-Umr[j])+dui*(Uei[j]-Umi[j])); end; setApproximationItem( Rg[i], i ); {restore si[i] value} end; end; setApproximationData( si , k ); end; procedure doMinimization; const mp1Max = maxPAR + 1; mp2Max = maxPAR + 2; m2Max = 2*( maxPAR + maxFUN ); m21Max = m2Max + 1; n2Max = 2*maxFUN; m1Max = maxPAR + n2Max; n1Max = n2Max + 1; mm1Max = maxPAR + n1Max; minDh : real = 0.001; {criterion of an exit from golden section method} var A : array [ 1 .. m1Max , 1 .. m21Max ] of real; B : array [ 1 .. m1Max] of real; Sx: array [ 1 .. m21Max] of real; Zt: array [ 1 .. maxPAR] of real; Nb: array [ 1 .. m1Max] of integer; N0: array [ 1 .. m21Max] of integer; a1, a2, dh, r, tt, tp, tl, cv, cv1, cl, cp : real; n2, n1, mp1, mp2, mm1, m1, m2, m21 : integer; ain : real; apn : real; iq : integer; k1 : integer; n11 : integer; ip : integer; iterI : integer; i,j,k : integer; label 102 ,103 ,104 ,105 ,106 ,107 ,108; begin n2:=2*nFreqs; n1:=n2+1; m1:=mCur+n2; mp1:=mCur+1; mp2:=mCur+2; mm1:=mCur+n1; m2:=2*( mCur+nFreqs ); m21:=m2+1; for k:=1 to m1Max do for i:=1 to m21Max do A[k,i]:=0; iterI:=0; 102: iterI:=iterI+1; getFunctional( 0 ); for i:=1 to nFreqs do b[i]:= -Fh[1,i]; getFunctional( derivType ); for k:=1 to mCur do begin Zt[k]:=Rg[k]; for i:=1 to nFreqs do begin A[i,k+1]:=Fh[k,i]; A[i+nFreqs,k+1]:=-A[i,k+1]; end; for i:=1 to nFreqs do B[i]:=B[i]+Rg[k]*A[i,k+1]; end; for i:=1 to nFreqs do B[i+nFreqs]:=-B[i]; for i:=n1 to m1 do B[i]:=Gr[1,i-n2]-Gr[2,i-n2]; for i:=1 to m1 do begin if i<=n2 then for k:=2 to mp1 do B[i]:=B[i]-A[i,k]*Gr[2,k-1]; A[i,1]:=-1; if i>n2 then begin A[i,1]:=0; for k:=2 to mp1 do if i-n2=k-1 then A[i,k]:=1 else A[i,k]:=0; end; for k:=mp2 to m21 do if k-mp1=i then A[i,k]:=1 else A[i,k]:=0; end; k1:=1; for k:=1 to n2 do if B[k1]>B[k] then k1:=k; for k:=1 to mp1 do A[k1,k]:=-A[k1,k]; A[k1,mCur+1+k1]:=0; B[k1]:=-B[k1]; for i:=1 to n2 do if i<>k1 then begin B[i]:=B[i]+B[k1]; for k:=1 to mm1 do A[i,k]:=A[i,k]+A[k1,k]; end; for i:=mp2 to m21 do begin Sx[i]:=B[i-mp1]; Nb[i-mp1]:=i; end; for i:=1 to mp1 do Sx[i]:=0; Sx[1]:=B[k1]; Sx[mp1+k1]:=0; Nb[k1]:=1; 103: for i:=2 to m21 do N0[i]:=0; 104: for i:=m21 downto 2 do if N0[i]=0 then n11:=i; for k:=2 to m21 do if ((A[k1,n11]<A[k1,k]) AND (k<>N0[k])) then n11:=k; if A[k1,n11]<=0 then goto 105; iq:=0; for i:=1 to m1 do if i<>k1 then begin if A[i,n11]>0 then begin iq:=iq+1; if iq=1 then begin Sx[n11]:=B[i]/A[i,n11]; ip:=i; end else begin if Sx[n11]>B[i]/A[i,n11] then begin Sx[n11]:=B[i]/A[i,n11]; ip:=i; end; end; end else if iq=0 then begin N0[n11]:=n11; goto 104; end; end; Sx[Nb[ip]]:=0; Nb[ip]:=n11; B[ip]:=B[ip]/A[ip,n11]; apn:=A[ip,n11]; for k:=2 to m21 do A[ip,k]:=A[ip,k]/apn; for i:=1 to m1 do if i<>ip then begin ain:=A[i,n11]; B[i]:=-B[ip]*ain+B[i]; for j:=1 to m21 do A[i,j]:=-ain*A[ip,j]+A[i,j]; end; for i:=1 to m1 do Sx[Nb[i]]:=B[i]; goto 103; 105: for k:=1 to mCur do Sx[k+1]:=Sx[k+1]+Gr[2,k]; a1:=0; a2:=1.; dh:=a2-a1; r:=0.618033; tl:=a1+r*r*dh; tp:=a1+r*dh; j:=1; 108: if j=1 then tt:=tl else tt:=tp; 106: for i:=1 to mCur do Rg[i]:=Zt[i]+tt*(Sx[i+1]-Zt[i]); getFunctional( 0 ); cv:=abs(Fh[1,1]); if nFreqs>1 then for k:=2 to nFreqs do begin cv1:=abs(Fh[1,k]); if cv<cv1 then cv:=cv1; end; if (j=1) or (j=3) then cl:=cv else cp:=cv; if j=1 then begin j:=2; goto 108; end; if dh<MinDh then goto 107; if cl>cp then begin a1:=tl; dh:=a2-a1; tl:=tp; tp:=a1+r*dh ; tt:=tp; cl:=cp; j:=4; end else begin a2:=tp; dh:=tp-a1; tp:=tl; tl:=a1+r*r*dh; tt:=tl; cp:=cl; j:=3; end; goto 106; 107: if (iterI < iterImax)AND(NOT saveResults( nStab,iterI )) then goto 102; end; End.
Приложение 2 - Удельная электрическая проводимость материалов Приведем сводку справочных данных согласно[7-9].
Приложение 4 - Abstract The inverse eddy current problem can be described as the task of reconstructing an unknown distribution of electrical conductivity from eddy-current probe voltage measurements recorded as function of excitation frequency. Conductivity variation may be a result of surface processing with substances like hydrogen and carbon or surface heating. Mathematical reasons and supporting software for inverse conductivity profiling were developed by us. Inverse problem was solved for layered plane and cylindrical conductors. Because the inverse problem is nonlinear, we propose using an iterative algorithm which can be formalized as the minimization of an error functional related to the difference between the probe voltages theoretically predicted by the direct problem solving and the measured probe voltages. Numerical results were obtained for some models of conductivity distribution. It was shown that inverse problem can be solved exactly in case of correct measurements. Good estimation of the true conductivity distribution takes place also for measurement noise about 2 percents but in case of 5 percent error results are worse. Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
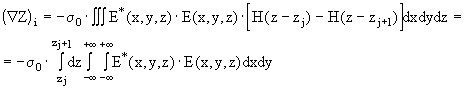
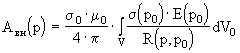
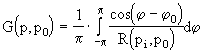
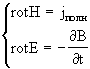
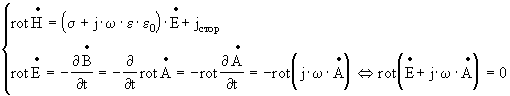
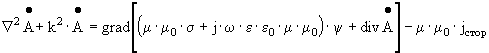
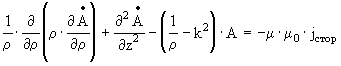
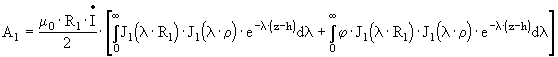
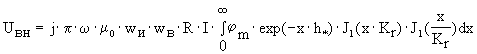
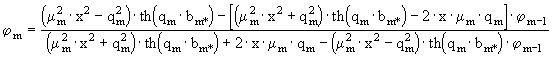
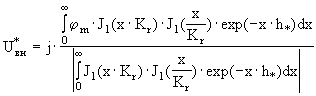
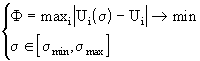
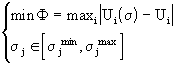
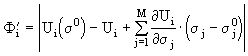
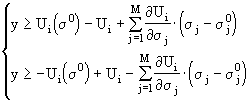
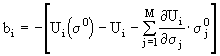
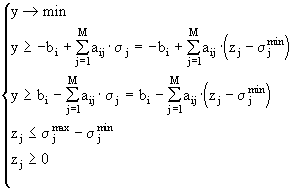
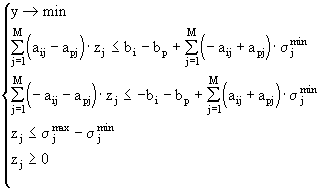
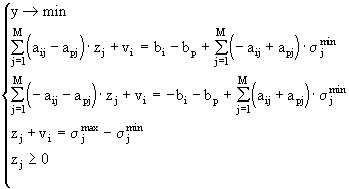
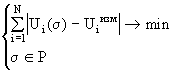
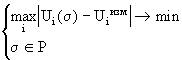
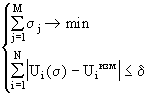
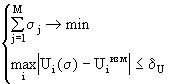
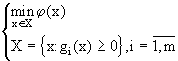
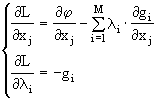
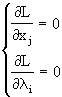
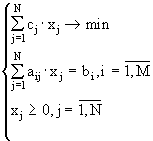
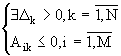
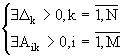
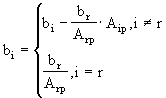
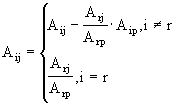
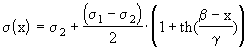
 Главная
Главная