Матричный анализ . Функции от матриц.
Df.
Пусть
Решение этой задачи известно, когда f(x) – многочлен:
Определение f(A) в общем случае.
Пусть m(x) – минимальный многочлен А и он имеет такое каноническое разложение
Пусть g(A)=h(A) (1), тогда многочлен d(x)=g(x)-h(x) – аннулирующий многочлен для А, так как d(A)=0, следовательно, d(x) делится на линейный многочлен, т.е. d(x)=m(x)*q(x) (2).
Тогда
Условимся m чисел для f(x) таких
Если множество f(Sp A) определено для f(x), то функция определена на спектре матрицы А. Из (3) следует, что многочлены h(x) и g(x) имеют одинаковые значения на спектре матрицы А. Наши рассуждения обратимы, т.е. из (3) Ю (3) Ю (1). Таким образом, если задана матрица А, то значение многочлена f(x) вполне определяется значениями этого многочлена на спектре матрицы А, т.е. все многочлены g i (x), принимающие одинаковые значения на спектре матрицы имеют одинаковые матричные значения g i (A). Потребуем, чтобы определение значения f(A) в общем случае подчинялось такому же принципу. Значения функции f(x) на спектре матрицы А должны полносильно определить f(A), т.е. функции, имеющие одни и те же значения на спектре должны иметь одно и то же матричное значение f(A). Очевидно, что для определения f(A) в общем случае, достаточно найти многочлен g(x), который бы принимал те же значения на спектре А, что и функция f(A)=g(A). Df. Если f(x) определена на спектре матрицы А, то f(A)=g(A), где g(A) – многочлен, принимающий на спектре те же значения, что и f(A),Df. Значением функции от матрицы А назовем значение многочлена от этой матрицы приСреди многочленов из С[x], принимающих одинаковые значения на спектре матрицы А, что и f(x), степени не выше (m-1), принимающий одинаковые значения на спектре А, что и f(x) – это остаток от деления любого многочлена g(x), имеющего те же значения на спектре матрицы А, что и f(x), на минимальный многочлен m(x)=g(x)=m(x)*g(x)+r(x). Этот многочлен r(x) называют интерполяционным многочленом Лагранжа-Сильвестра для функции f(x) на спектре матрицы А.
Замечание.
Если минимальный многочлен m(x) матрицы А не имеет кратных корней, т.е.
Пример: Найти r(x) для произвольной f(x), если матрица
m x =f n (x)=d n (x)/d n-1 (x)=x n Ю 0 – n –кратный корень m(x), т.е. n-кратные собственные значения H 1 .
Свойство № 1. Доказательство: Пусть характеристический многочлен матрицы А имеет вид:
Сделаем замену в равенстве:
Равенство (*) справедливо для любого множества f(x), поэтому заменим многочлен f(x) на
Слева мы получили характеристический многочлен для матрицы f(A), разложенный справа на линейные множители, откуда следует, что
ЧТД.
Свойство № 2.
Пусть матрица
Доказательство:
Т.к. функция f(x) определена на спектре матрицы А, то существует интерполяционный многочлен матрицы r(x) такой, что
ЧТД.
Свойство № 3.
Если А и В подобные матрицы,
Доказательство:
Т.к. А и В подобны, то их характеристические многочлены одинаковы
Ю
одинаковы и их собственные значения, поэтому значение f(x) на спектре матрицы А совпадает со значение функции f(x) на спектре матрицы В, при чем существует интерполяционный многочлен r(x) такой, что f(A)=r(A),
ЧТД.
Свойство № 4.
Если А – блочно-диагональная матрица
Следствие:
Если
Случай № 1.
Пусть дана
Пусть f(x) – функция, определенная на спектре матрицы А и значениями этой функции на спектре будут
Построим:
Обратим внимание, что
Пример: Построить интерполяционный многочлен Лагранжа-Сильвестра для матрицы
Тогда для функции f(x), определенной на спектре матрицы А, мы получим:
Возьмем
Случай № 2.
Характеристический многочлен матрицы А имеет кратные корни, но минимальный многочлен этой матрицы является делителем характеристического многочлена и имеет только простые корни, т.е.
Случай № 3. Рассмотрим общий случай. Пусть минимальный многочлен имеет вид:
где m 1 +m 2 +…+m s =m, deg r(x)<m. Составим дробно-рациональную функцию:
Обозначим:
где
Если в (**) положить
Для того, чтобы найти a k3 надо (**) продифференцировать дважды и т.д. Таким образом, коэффициент a ki определяется однозначно. После нахождения всех коэффициентов вернемся к (*), умножим на m(x) и получим интерполяционный многочлен r(x), т.е.
Пример: Найти f(A), если
Найдем минимальный многочлен матрицы А:
Проверим, определена ли функция на спектре матрицы А
Умножим (*) на (х-3)
при х=3
Умножим (*) на (х-5)
Таким образом,
Пример 2.
Если
Найдем минимальный многочлен матрицы А:
d 2 (x)=1, тогда минимальный многочлен
Рассмотрим f(x)=sin x на спектре матрицы:
Умножим (*) на
Умножим (*) на
Вычислим g , взяв производную (**):
Итак,
ЧТД. Пример 3.
Пусть f(x) определена на спектре матрицы, минимальный многочлен которой имеет вид
Решение: По условию f(x) определена на спектре матрицы А Ю f(1), f’(1), f(2), f ‘(2), f ‘’ (2) определены.
Используем метод неопределенных коэффициентов:
Если f(x)=ln x f(1)=0 f’(1)=1 f(2)=ln 2 f’(2)=0.5 f’’(2)=-0.25
4. Простые матрицы.
Пусть матрица
Обозначим множество векторов удовлетворяющих собственному значению
Теорема.
Если квадратная матрица А имеет собственное значение
DF
. Размерность
В свете этого определения теорема переформулируется следующим образом: Теорема. Алгебраическая кратность собственного значения не меньше его геометрической кратности.
DF
. Матрица
Из линейной алгебры следует, что матрица
Если матрица А простая, тогда существует n линейно независимых собственных векторов x
1
, x
2
, …,x
n
таких, что
Замечание.
Обратим внимание на то, что собственные значения А и А’ совпадают. Действительно, собственные значения для А’ это значения
Рассмотрим следующую конструкцию: если матрица А простая, то существует n линейно независимых собственных векторов x
1
, x
2
, …, x
n
и существует n линейно независимых собственных векторов y
1
, y
2
,…,y
n
, где x
1
, x
2
, …, x
n
такие, что
Запишем равенство (1) в виде
DF
. Множества векторов x
1
, x
2
, …, x
n
и y
1
, y
2
,…,y
n
удовлетворяющие условию
Учитывая равенство (**) и определение делаем вывод: множества левых и правых собственных векторов простой матрицы А квазиортогональны и
Очень важной для матриц является следующая теорема:
СПЕКТРАЛЬНАЯ ТЕОРЕМА.
Если А – простая матрица порядка n над полем С и p(x) многочлен из кольца C[x], и x
1
, x
2
, …, x
n
и y
1
, y
2
,…,y
n
– множества правых и левых собственных векторов матрицы А, то
Следствие . Сопутствующие матрицы обладают следующими свойства:
Пример. Показать, что матрица
Решение:
существуют 2 линейно независимые правые и левые системы собственных векторов. Найдем правые собственные векторы:
Найдем левые собственные векторы:
Найдем сопутствующие матрицы:
5.Спектральное разложение функции f(A). Спектральное разложение для f(A) имеет важное значение и очевидно тесно примыкает к спектральной теореме для простых матриц.
Пусть дана матрица
Теорема.
Если
Доказательство:
заметим, что
ЧТД. Опишем следующие свойств компонентных матриц, которые в некоторой степени обобщают свойства сопровождающих матриц.
Теорема
. Компонентные матрицы
. Замечание. Для того, чтобы найти компонентные матрицы для f(x) определенной на спектре матрицы А необходимо и достаточно знать базисные многочлены, входящие в интерполяционный многочлен, однако нахождение интерполяционного многочлена f(x) связано с некоторыми трудностями, а поэтому будем вычислять компонентные матрицы подбирая соответствующим образом системы функций.
Пример: Найти компоненты для матрицы
Пусть f(x) определена на спектре А, тогда согласно спектральной теореме
E=1Z 11 +0Z 12 +1Z 21 =Z 11 +Z 21
A-4E=0Z 11 +1Z 12+ (-2 ) Z 21 =Z 12 -2Z 21
(A-4E) 2 =4Z 21
Таким образом, для любой функции f(x), определенное на спектре матрицы А
Пример 2. Найти компоненты для матрицы
Найдем минимальный многочлен матрицы А.
E=Z 11 +Z 21 +Z 31
(A+E)=2Z 21 +Z 31 +Z 12
(A+E) 2 =4Z 21 +Z 31
A-E=-2Z 11 +Z 12 -Z 31
1. f(x)=1 E=Z 11 +Z 21 +Z 31 2. f(x)=x+1 A+E=Z 11 Z 22 +2Z 31 3. f(x)=(x+1) 2 (A+E) 2 =Z 11 +4Z 31 4. f(x)=x-1 (A-E)=-Z 11 -2Z 21 +Z 22
Z 31 =A -Z 22 =(A+E) 2 -E-3A Z 12 =Z 22 Z 11 =(E-A)-Z 22 6.Определенные матрицы. Эрмитовы и квадратичные матрицы. Пусть А – эрмитова матрица (А * =А). Рассмотрим функцию h(x) – действительная функция комплексного аргумента.
Рассмотрим:
DF
. Функция
Очевидно, что если А – действительная симметрическая матрица, то в этом случае получаем квадратичную форму
Для каждой эрмитовой (квадратичной) формы инвариантами являются: ранг (число не нулевых коэффициентов в квадратичной форме нормального вида совпадающих с рангом матрицы А), p (индекс) – число положительных коэффициентов в квадратичной форме нормального вида, оно совпадает с числом положительных собственных значений, сигнатура . Эти числа r, p, гр-r не зависят от тех преобразований, которые совершаются над данными формами. В дальнейшем ограничимся рассмотрением только квадратичных форм. Нас интересуют 2 семейства матриц.
DF
. Действительная симметрическая матрица А называется
положительно определенной
, если
DF
. Действительная симметрическая матрица А называется
неотрицательно определенной
, если
Оба типа матриц относятся к классу определенных матриц. Заметим, что положительно определенная матрица невырожденная, т.е. если предположить, что она вырожденная, то
Теорема № 1.
Действительная симметрическая матрица n-го порядка будет определенной ранга
Теорема № 2. Действительная симметрическая матрица положительна определена тогда и только тогда, когда все ее главные миноры положительны. Теорема № 3 . Действительная симметрическая матрица положительно определена тогда и только тогда, когда все ее главные миноры положительны. 7.Неотрицательные матрицы.
DF
. Матрица
Квадратные матрицы такого типа возникают во множестве задач и это определяющее свойство приводит к сильным результатам об их строении. Теорема Фробениуса-Перона является основным результатом для неотрицательных матриц.
Пусть матрицы
Вспомним матрицу перестановки
DF
. При
Понятие приводимости имеет значение при решении матричных уравнений
Интересно, что явление приводимости не связано с величиной матрицы, а зависит лишь от расположения нулевых элементов в матрице. В связи с этим, используют идею направленного графа матрицы, которую можно взять в качестве характеризации неприводимости матрицы. Наметим первые шаги тоерии и получим вторую характеризацию неприводимости матриц.
DF
. Пусть р
1
, р
2
, …, р
n
– n различных точек комплексной плоскости и
Например:
DF
. Говорят, что любой направленный граф связен, если для каждой пары точек
Легко доказать, что квадратная матрица неприводима тогда и только тогда, когда ее граф является связным. 8.Теорема Фробениуса-Перона.
Очевидно, что если
Лемма № 1.
Если матрица
Доказательство:
Если взять произвольный вектор
Учитывая, что
Для следующего вектора повторим рассуждения и т.д. В итоге получим, что для некоторого ненулевого вектора y
ЧТД.
Для ненулевой неприводимой матрицы А рассмотрим действительную функцию r(x), определенную для ненулевых векторов
Очевидно, что r(x) инвариантна относительна замены x на
Однако, r(x) может иметь разрывы в точках, где координата x обращается в 0, поэтому рассмотрим множество векторов
Обозначим через
Замечание. Могут существовать и другие векторы в L для которых r(x) принимает значение r, поэтому любой такой вектор называется экстремальным для матрицы А (Az=rz). Интерес к числу r объясняется следующим результатом.
Лемма № 2.
Если матрица
Основным результатом является теорема Фробениуса-Перона для непрерывных матриц.
Теорема Фробениуса-Перона
. Если матрица
Эта теорема была опубликована в 1912 году Фробениусом и явилась обобщением теоремы Перона, которая является следствием. Теорме Перона (следствие). Положительная квадратная матрица А имеет положительное и действительное собственное значение r, имеющее алгебраическую кратность 1 и превосходит модули всех других собственных значений матрицы А. Этому r соответствует положительный собственный вектор. Используя теорему Фробениуса-Перона, можно найти максимальное действительное значение матрицы, не используя характеристического многочлена матрицы. Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
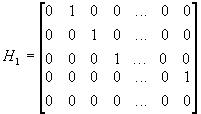 . Построим f(H
1
). Найдем минимальный многочлен H
1
– последний инвариантный множитель [xE-H
1
]:
. Построим f(H
1
). Найдем минимальный многочлен H
1
– последний инвариантный множитель [xE-H
1
]:
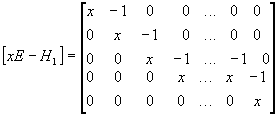 , d
n-1
=x
2
; d
n-1
=1;
, d
n-1
=x
2
; d
n-1
=1;

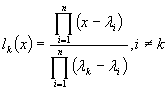 .
.
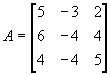 .
.
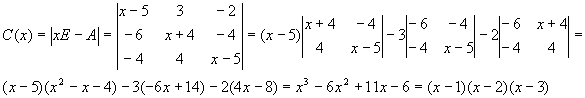 Построим базисные многочлены:
Построим базисные многочлены:
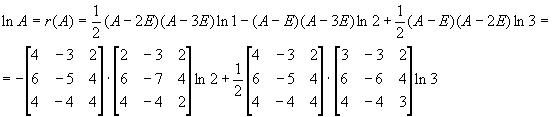 .
.
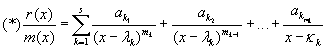
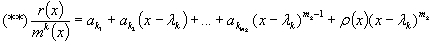
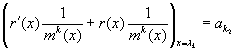
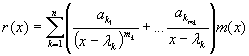 .
.
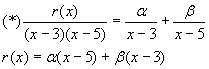

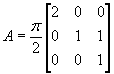 , то доказать, что
, то доказать, что
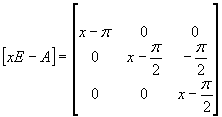 - характеристический многочлен.
- характеристический многочлен.
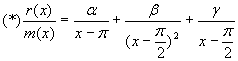 .
.
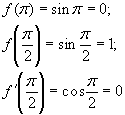 Ю
функция является определенной на спектре.
Ю
функция является определенной на спектре.
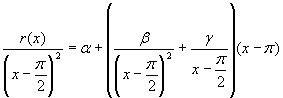 Ю
Ю
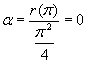 .
.
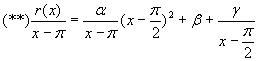
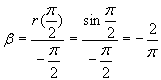 .
.
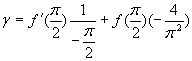 , т.е.
, т.е.
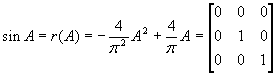 .
.
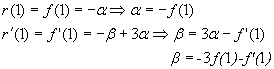
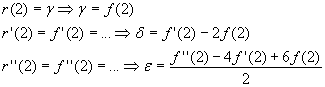
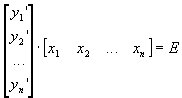 , т.е.
, т.е.
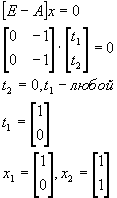
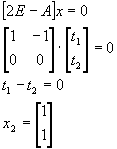
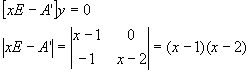
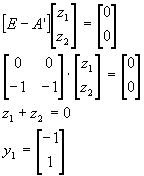
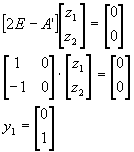
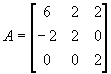 .
.
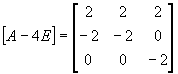
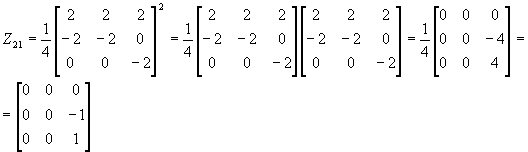
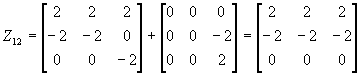
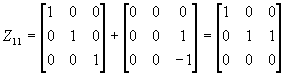 .
.
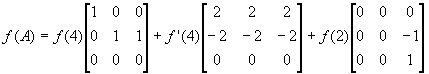
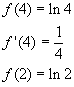
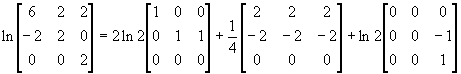
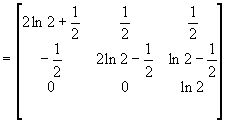 .
.
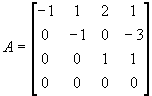 .
.
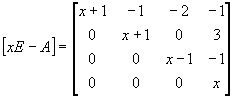
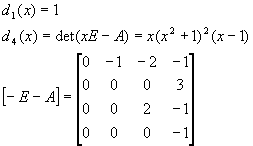
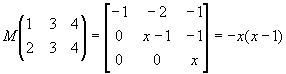
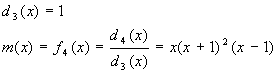
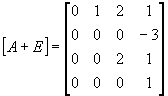
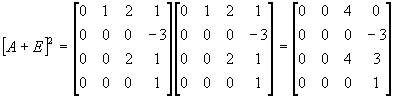
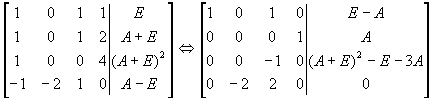
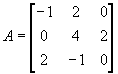
 Главная
Главная