Экспериментальные исследования диэлектрических свойств материалов
Цель работы: определение диэлектрической проницаемости и поляризационных характеристик различных диэлектриков, изучение электрических свойств полей, в них исследование линейности и дисперсии диэлектрических свойств материалов. Теоретическая часть: Схема экспериментальной установки.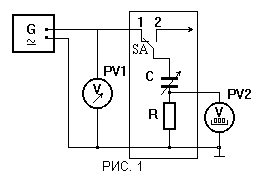 
В эксперименте используются следующие приборы: два вольтметра PV1 (стрелочный) и PV2 (цифровой) , генератор сигналов низкочастотный, макет-схема, на которой установлен резистор R=120 Ом, конденсатор, состоящий из набора пластин различных диэлектриков (толщиной d=2 мм) . Собираем схему, изображенную на РИС. 1. Ставим переключатель SA в положение 1. Подготавливаем к работе и включаем приборы. Подаем с генератора сигнал частоты f = 60 кГц и напряжением U=5 В, затем по вольтметру PV1 установить напряжение U1=5 В. Далее, вращая подвижную пластину, измеряем напряжение U2 для конденсатора без диэлектрика и 4-x конденсаторов с диэлектриками одинаковой толщины. При этом напряжение U1 поддерживаем постоянным.
Напряженность поля между пластинами в вакууме Е
0
вычисляется по формуле:
Экспериментальная часть:
В данной работе используются формулы:
Опыт №1. Измерение диэлектрической проницаемости и характеристик поляризации материалов. U 1 = 5В, R=120Ом, f=60 кГц, d=0,002м.
Для гетинакса подсчитаем:
Расчет погрешностей:
R=120Ом, f=60 кГц, d=0,002м.
График зависимости e = f(E) - приблизительно прямая, так как диэлектрическая проницаемость не зависит от внешнего поля. Опыт № 3. Исследование зависимости диэлектрической проницаемости среды от частоты внешнего поля. U 1 = 5В, R=120Ом.
По графику зависимости e = F(f) видно, что диэлектрическая проницаемость среды не зависит от частоты внешнего поля. График зависимости Х С =F(1/f) подтверждает, что емкостное сопротивление зависит от 1/f прямо пропорционально. Опыт № 4. Исследование зависимости емкости конденсатора от угла перекрытия диэлектрика верхней пластиной. U 1 = 5В, R=120Ом, f=60 кГц, d=0,002м, r=0,06м, n=18.
Опыт № 5. Измерение толщины диэлектрической прокладки. U 1 = 5В, R=120Ом, f=60 кГц. Схема конденсатора с частичным заполнением диэлектриком. U 2 (стеклотекстолит тонкий) =0,051В, U 2 (стеклотекстолит толстый) =0,093В, U 2 (воздух) =0,039В.
Вывод: На этой работе мы определили диэлектрическую проницаемость и поляризационные характеристики различных диэлектриков, изучили электрические свойства полей, в них исследовали линейность и дисперсность диэлектрических свойств материалов. Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
где
При внесении пластины в это поле диэлектрик поляризуется и на его поверхности появляются связанные заряды с поверхностной плотностью
. Эти заряды создают в диэлектрике поле
, направленное против внешнего поля
, и имеет величину:
. Результирующее поле:
. В электрическом поле вектор поляризации:
, где c - диэлектрическая восприимчивость вещества. Связь модуля вектора поляризации с плотностью связанных зарядов:
.
относительная диэлектрическая проницаемость диэлектрика. Вектор электрической индукции
. Этот вектор определяется только свободными зарядами и вычисляется как
. В рассматриваемой задаче на поверхности диэлектрика их нет. Вектор D связан с вектором Е следующим соотношением
.
, где S - площадь пластины конденсатора, d - расстояние между ними. Диэлектрическая проницаемость материала:
. Для емкости конденсатора имеем:
, где U
1
- напряжение на RC цепи, U
2
- напряжение на сопротивлении R, f - частота переменного сигнала. В плоском конденсаторе напряженность связана с напряжением U
1
как:
С
В
=176 пкФ; С
СТ
=429 пкФ; С
ФП
=270 пкФ; С
ГН
=393 пкФ; С
ОС
=336 пкФ;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
(так как
) .
;
Опыт № 2.
Исследование зависимости e = f(E) .
;
;
;
;
;
;
;
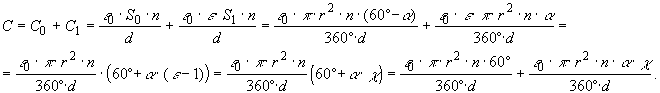
Главная