Комплексные числа
§ 1.Тема. Некоторые определения и обозначения. Определение. Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Если неизвестная функция зависит от одной переменной, то это обыкновенное дифференциальное уравнение, иначе - уравнение в частных производных. Определение. Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения. Определение. Дифференциальное уравнение называется линейным, если производные и сама неизвестная функция входят в уравнение линейным образом.
Пусть выбран любой
Определение.
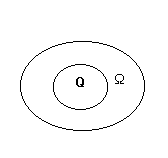
Открытое, связное множество
По умолчанию будем считать область ограниченной.
Через
Определение.
для
D
- проекция данного множества на плоскость
Можно разбить поверхность на части, в каждой части можно одну координату выразить через другие непрерывно дифференцируемой функцией.
Аналогично:
§ 2. Классификация линейных уравнений в частных производных второго порядка.
1.Если
Ex: Уравнение Пуассона
2.Если
Ex:
Для уравнения Лапласа:
Для волнового уравнения:
3.Если
Ex:
4.Если
Ex:
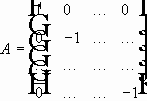
Определение. Каноническим видом линейного дифференциального уравнения в частных производных называется такой вид, когда матрица A является диагональной. Приведение к каноническому виду. 1) y=y(x), то:
Уравнение (1) в новой системе координат:
Матрица Якоби:
В результате:
Ex:
гиперболическое уравнение.
Замечание: тип уравнения может быть различный в различных точках. § 3.Постановка начальных и краевых задач для уравнений в частных производных. Задача Коши для волнового уравнения:
Уравнение теплопроводности
Уравнение Пуассона
Определение. Если малые изменения правой части уравнения приводят к большим изменениям в решении, то задача считается некорректной.
(6)(7.1) - первая краевая задача, задача Дирихле. (6)(7.2) - вторая краевая задача, задача Неймана. (6)(7.3) - третья краевая задача. Волновое уравнение.
(8) (9) (10) (11.1) - смешанные (11.2) задачи (11.3) (краевые задачи)
На
На боковой поверхности - краевые задачи. Параболическое уравнение.
(12) (13) (14 .1) - первая, вторая и третья смешанные задачи (14.2) для уравнения (14.3) теплопроводности. (14.1) - на границе задана температура; (14.2) - задан тепловой поток; (14.3) - задан теплообмен с окружающей средой. § 4. Решение смешанных задач для волнового уравнения методом Фурье (разделением переменных). Первая смешанная задача.
Собственные значения (5) - (6) вещественны, имеют конечную кратность.
В симметричной матрице собственные вектора, соответствующие разным собственным значениям, попарно ортогональны.
Пусть функции
тогда и
u(t,x)
можно разложить по базису
Почленно дифференцируем ряд 2 раза:
Путём разложения решения в ряды по собственным функциям задачи алгебраизуем задачу, получаем счётное число обыкновенных дифференциальных уравнений.
(7) (8) (9) - задача. Решим однородное уравнение для (7):
- общее решение однородного уравнения (7)
В результате:
Подставим (8) и (9) в решение:
т.е.
Замечание: не обоснована сходимость рядов. § 5.Решение смешанных задач уравнения теплопроводности методом Фурье (разделения переменных).
Рассмотрим функцию:
Если
Введём
Свойства
1)
2)
3)
Доказательство.
4)
Обозначим:
Интеграл по x бесконечно дифференцируем.
Если
Носитель функции принадлежит области интегрирования, и:
Если
Свойства функции
Пространство
Определение.
Пусть
-
-
Вводится
Утверждение (без доказательства).
Вводится
Свойства пространства
Теорема 1.
Множество финитных бесконечно дифференцируемых функций всюду плотно в пространстве
Доказательство.
Множество ступенчатых функций плотно в
Множество линейных комбинаций характеристических функций всюду плотно в
Доказать: любую характеристическую функцию измеримого множества можно сколь угодно точно аппроксимировать финитными функциями. Любое измеримое множество сколь угодно точно может быть аппроксимировано открытыми областями.
Доказать: характеристическую функцию
Рассмотрим
Значит,
Аппроксимация получена. Теорема 2.
Множество непрерывных функций всюду плотно в пространстве
Определение 2.
Пусть
f
- непрерывна в среднеквадратичном, если
Теорема 3.
Любая функция из
Доказательство.
Пусть
Оценим:
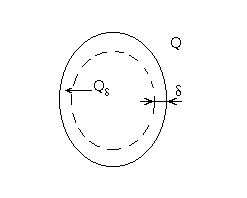
При сдвиге supp сдвигается в пределах шара радиуса 2a.
Теорема доказана. Определение 3.
Свойства:
Теорема 4.
Любая функция из
Доказательство.
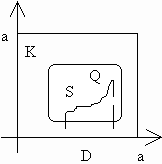
От
Q
к
При
Возьмем любые две функции:
Определение.
Определение 1.
Пусть
Теорема 1. Обобщённая производная определяется единственным образом. Доказательство.
Предположим противное:
(2),(3) - тождество для
Теорема 2. Обобщённые производные не зависят от порядка дифференцирования. Доказательство - из интегрального тождества (1). Примеры обобщённых производных. Ex 1.
По определению:
Пусть
Ex 2.
Покажем, что обобщённой производной не существует.
Пусть
где
1) пусть
2) пусть
Вывод:
Вывод:
Теорема 3.
Пусть
1.
если
2. Если к тому же
Доказательство.
Выберем
h
так, чтобы
Подсказка: если функция финитна, то её носитель - внутри области. Если функцию умножить на срезающую, то ничего не изменится. Теорема 4.
Утверждение.
Пусть
Пусть
Теорема 5.
Пусть
существует обобщённая производная
Пространство Соболева. Определение.
Обозначения:
Введём
Утверждение.
Теорема 1.
Доказательство.
Интегральное тождество для
Из сильной сходимости следует слабая:
Вывод: пространство полное. Свойства пространств Соболева.
1.
2.Если
3.Если
4.Если
если
5.
Пусть
Пусть
Утверждение. Невырожденная, гладкая замена переменных сохраняет принадлежность функции пространству Соболева.
6.Обозначим
Множество бесконечно дифференцируемых функций замыкания куба является всюду плотным в
Доказательство.
Раздвинем область, возьмём
Оценим:
Выберем
Разбиение единицы. Теорема.
Пусть
Используется для локализации свойства: U имеет свойство на
Доказательство.
Возьмём
Для каждой выбранной y построим:
Обозначим:
Определим:
Получили:
Если
Знаменатель в 0 не обращается. Построена
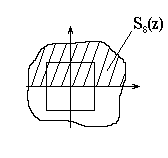
Теорема о разбиении единицы доказана. Теорема о продолжении функции. Частный случай - продолжение из прямоугольников.
Продолжение функции из
Лемма 1.
1.Определить функцию.
2
.Проверить условие сливания: совпадание значений функции и её производных по
Доказательство.
Определим
Коэффициенты
Значит, функция непрерывна. Теперь - доказательство совпадения производных.
Выполняется одно уравнение из (3), и:
Значит:
Неравенство (1) очевидно через определение нормы в
Замечание: из доказательства и свойства (6) пространств Соболева следует: можно перейти к
Замечание: в силу того, что множество бесконечно дифференцируемых функций в замыкании куба всюду плотно в пространстве
Лемма 2.
Теорема о продолжении функции.
Пусть
1)
2)
3)
Замечание.
Лемма 1 - рассмотрены кубики, в теореме: из
Q
на
Доказательство.
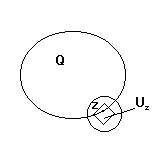
В окрестности каждой точки границы:
Пусть в
O(z)
граница задаётся уравнением
Введём новые переменные:
Преобразование:
Во что перейдёт множество:
Вырезали куб
Результат преобразования
Прообраз куба
Покроем границу кубиками Vi и выберем конечное подпокрытие. (Tju)(y) = u(x(y)) (xVj) - переход от x к y,
переход от
y
к
x
:
Введём :
Свойства оператора продолжения: 1. F(x) - ограниченный оператор;
2. Т.к.
Доказать:
F(x)=f(x)
,если
Замечание.
Теорема 1 остаётся справедливой для пространств
Теорема 2.
Пусть
Доказательство.
Рассмотрим произвольную функцию
F
-продолжение
f.
Так как
F
- финитная в , то
Сепарабельность пространств Соболева. Теорема.
Пусть
Построениe счётного всюду плотного множества. Доказательство.
Рассмотрим
Аппроксимируем функцию
F
. Множество финитных, бесконечно дифференцируемых функций (в силу свойств осреднений) всюду плотно в пространстве финитных функций
Очевидно :
Где коэффициенты :
Пусть H - сепарабельное гильбертово пространство. Определение.
Функции
Утверждение.
В каждом сепарабельном гильбертовом пространстве существует ортонормированный базис, т.е. такая система
Разложение по этому базису единственно, и :
Равенство Парсеваля.
Пространство
Разложение в сходящийся ряд :
Определим вид коэффициентов Фурье:
проинтегрируем по частям и получим :
Получаем :
F можно точно аппроксимировать линейными комбинациями экспонент. Искомое множество - линейное пространство экспонент с рациональными коэффициентами. След функции из H k (Q).
Для функции из
Если
определение следа функции на (n-1)- мерной поверхности.
Рассмотрим
Пусть
Для любой непрерывной функции след - её значение на поверхности, однозначно продолженое по непрерывности.
Так как f=0 вне области Q , то по формуле Ньютона-Лейбница :
Оценим :
Обе части умножим на
f - финитная.
Так как
Существует последовательность
Отсюда следует фундаментальность последовательности следов в
Перейдём к пределу, получим :
Утверждение.
Определение
Доказательство.
Пусть есть две последовательности
Пусть
Следовательно, должны совпадать два предела в
Рассмотрим
Значит :
Если функция непрерывна в
Формула интегрирования по частям.
Пусть Q- ограниченная,
Теорема Реллиха-Гординга.
Если
Пространство Соболева с большим показателем дифференцируемости k компактно вложено в ространство Соболева с меньшим показателем.
Пусть
Множества, ограниченные в
Определение. Предкомпактными называются такие множества, замыкания которых компактны.
Из любой ограниченной последовательности функций из
Или : Для
Доказательство.
1. Продолжим функции
Оператор продолжения ограничен, и :
Т. к. множество финитных, бесконечно дифференцируемых функций всюду плотно в пространстве функций
Используем преобразование Фурье :
В силу финитности :
Оценим по неравенству Коши-Буняковского:
Свойство. В гильбертовом пространстве из ограниченной последовательности можно выделить слабо сходящуюся подпоследовательность.
В качестве
Докажем, что
Так как последовательность
исходя из теоремы Планшереля (в обратную сторону) и свойств преобразования Фурье :
Выбором R, интеграл
Если
Формула интегрирования по частям
В уравнении (2) перейдем к пределу при
Пространство
Определение.
Назовём пространством
Если есть
Если
Теорема.
Определение. Эквивалентные нормы. Пусть H - гильбертово пространство со скалярным произведением ( . , . ).
Скалярное произведение
Из эквивалентности скалярных произведений можно пользоваться любым. Теорема 2.
В пространстве
Доказательство.
Надо доказать :
Доказательство от противного.
Будем считать, что
Имеем противоречие.Теорема доказана. Обобщенное решение задачи Дирихле для уравнения Пуассона.
Пусть
Определение.
Функция
При исследовании обобщенных решений
Лемма.
Существует линейный ограниченный оператор
При этом
По определению :
f -ограничен, следовательно применим теорему Рисса :
F - линейно зависит от u.
Компактность очевидна по теореме Реллиха-Гординга.
Самосопряженность доказана.
Теорема.
Для любой функции
Задача Дирихле для уравнения Пуассона корректна, т.е. существует единственное решение непрерывно зависящее от правой части. Доказательство.
Собственные значения и собственные функции оператора Лапласа.
Определение.
Функция
Теорема. 1. Собственные значения задачи (1) (2), являются вещественными, положительными, изолированными, имеют конечную кратность, и :
2.Существует ортонормированный базис в
3.
Доказательство. Интегральное тождество (3) можно записать в виде :
Эквивалентная задача :
Теорема 1.
Если
Теорема 2.
Пусть
{0} всегда принадлежит спектру компактного оператора. Теорема 3.
Пусть
Для удобства
Значит :
Так как
Значит :
Рассмотрим задачу :
где
Краевые условия :
Теорема 1.
Если однородная краевая задача имеет единственное тривиальное решение, то неоднородное неоднородная краевая задача (1) (2) имеет единственное решение для
2.
Если (3) (4) имеет нетривиальное решение , то (1) (2) разрешима тогда и только тогда, когда
3 . Задачи (3) (4) и (5) (6) имеют одинаковое число линейно независимых решений. Теорема Фредгольма. Рассмотрим уравнения
где I - единичный оператор в H, C - компактный оператор в H.
1. Если однородное уравнение (11) имеет единственное тривиальное решение, то для
2. Если уравнение (11) имеет нетривиальное решение, то уравнение (10) разрешимо тогда и только тогда, когда
3.
Оценим член :
Изучим член :
Значит :
(1) (2)
(3) (4)
(5) (6)
Доказана первая часть теоремы.
Пусть (3) (4) имеет нетривиальное решение, тогда
Т.е.
Теорема доказана. Разложение решения задачи Дирихле для уравнения Пуассона в ряд по собственным функциям.
Конечноразностные операторы. Цель : Аппроксимация обобщенных производных конечноразностными операторами.
Пусть
Аналог формулы интегрирования по частям :
Обозначим :
Теорема.
Пусть
1) если
и при этом :
2) Если для
Доказательство.(1ая часть теоремы) Из теорем об аппроксимации функции f и её обобщённой производной осреднениями функции f и её обобщенной производной сооответственно следует, что достаточно доказать часть теоремы для финитной бесконечно диффреренцируемой функции.
(применив неравенство Коши-Буняковского)
По теореме Фубини имеем неравенство :
Доказательство. (2-ая часть. )
Значит :
Доказательство теоремы 2.
Пусть
Q - симметрично относительно
Обозначим :
Теорема 2.
Пусть
1) если
2) если
Указание. Для доказательства рассмотреть :
По определению обобщённой производной в (1) получаем :
Локальная гладкость обобщённых решений.
Обобщённое решение :
Теорема 1.
Для любого
независимо от гладкости границы, если правая часть из
Доказательство.
Достаточно доказать, что
Обозначим
В качестве v для (3) возьмём :
- финитная, бесконечно дифференцируемая.
Подставим v в (3) :
(умножение u на срезающую функцию для локализации свойства в шаре )
Введём конечноразностный оператор. Пусть
Представим (5) в виде :
Оценим :
По неравенству Коши-Буняковского :
где
Подставляем в решение в качестве пробной функции :
Результат :
В силу 2-ой части теоремы 1 (см. стр. ...) :
u
имеет обощённые производные
Обобщение Теоремы на случай произвольной гладкости правой части. Теорема 2.
Пусть
Гладкость обобщённых решений эллиптических задач вблизи границ.
Теорема 1.
Пусть
Доказательство.
Доказать, что
Пусть в окрестности X и Y граница создаётся уравнением :
Не ограничивая общности рассуждений будем считать, что граница плоская. Введём срезающую функцию :
Подставим v в (3), получим :
Введём конечноразностный оператор. Пусть
При этом :
Представим (5) в виде :
Через неравенство Коши-Буняковского, получим :
где
Подставляем в решение в качестве пробной функции :
В силу 2-ой части теоремы 1 (см. стр. ...) :
u имеет обощённые производные
Лемма.
Пусть
Будем считать :
Значит :
Теорема 2.
Пусть
Теорема "вложения" Соболева.
Определение. Непрерывность оператора наложения - это
Доказательство (теоремы).
если
Доказательство (1) будет следовать из доказательства (2) и
Пусть (3) доказана для любой финитной, гладкой
(
Замечание.
Предел в смысле почти всюду :
Остаётся доказать (3) для любых финитных, бесконечно дифференцируемых в функций.
Преобразование Фурье :
где
умножим и разделим на
Докажем, что интеграл конечен :
Где
Теорема полностью доказана. Обобщённые и классические решения.
Функция
Теорема 1.
Если
Доказательство.
Пусть
Теорема 2.
Пусть
Доказательство.
Теорема 3.
Пусть
Доказательство.
Теорема 4.
Пусть
Доказательство.
Если
По теореме вложения:
Задача Неймана для уравнения Пуассона.
Определение. Функция называется обобщенным решением задачи (1) (2), если:
Пусть
Теорема 1.
Задача (1) (2) разрешима тогда и только тогда , когда правая часть уравнения (1) ортогональна константам, т.е:
Лемма. Существует линейный ограниченный оператор , такой, что:
1)
2)
Доказательство - аналогично.
Рассмотрим однородное уравнение:
для однородной задачи (1) (2)
имеет нетривиальное решение.
По определению обобщенного решения :
Теорема доказана. Рассмотрим уравнение:
Теорема 2.
1. Если задача (3) (4) имеет единственное решение, то задача (1) (2) также имеет единственное решение для
2. Если задача (3) (4) имеет нетривиальное решение, то задача (1) (2) разрешима тогда и только тогда, когда
3. Размерности подпространств в решениях задач (3) (4) и (5) (6) совпадают и конечны. Задача Неймана:
Рассмотрим задачу на собственные значения:
1. Собственные значения оператора Лапласа с "-" с условиями Неймана вещественные, конечнократные, неотрицательные и состоят из следующих чисел:
2. Соответствующие собственные функции
3.
Доказательство.
Первая часть теоремы доказана.
По Гильберту-Шмидту строится
Теорема 3 доказана. Задача Дирихле - однозначная разрешимость. Теорема 4 о гладкости решения задачи Неймана.
Пусть
Доказательство - аналогично теореме 3. Теорема 5.
Пусть граница
Теорема 6.
Пусть граница
Доказательство.
Обобщенное решение:
Уравнение (1) выполняется почти всюду в Q , и:
Метод Ритца. Суть: сведение бесконечномерного случая к конечномерному.
Рассмотрим:
l(u)
- линейный, ограниченный функционал в
Найдем минимум квадратичного функционала:
Найдется
Теорема 1.
Существует единственный
Доказательство. Возьмем любую минимизирующую последовательность. Очевидно:
Почленно сложим соотношения с "+" и с "-":
Доказано: последовательность
Доказано: если
Доказательство единственности от противного: пусть есть второй минимальный элемент; составим минимизирующую последовательность:
Она не сходится, значит, второй минимальный элемент не существует.
Пусть
Обозначим через
Рассмотрим
Необходимое условие экстремума:
Система алгебраических уравнений (1) имеет единственное решение, т.к. её определитель (Грама) отличен от 0.
Обозначим решение
Теорема 2.
Последовательность Ритца является минимизирующей, и, следовательно, сходится к минимизирующему элементу
u
:
Доказательство.
Т.к.
Рассмотрим значение
Таким образом:
Теорема 3.
Доказательство.
Необходимость: пусть
u
- минимизирующий элемент; возьмем
что и требовалось доказать. Достаточность: пусть выполняется (2), то рассмотрим:
т.е.
Выводы. 1. Существует единственный минимизирующий элемент - предел минимизирующей последовательности ( последовательности Ритца). 2. Минимизация функционала связана с обобщенным решением краевой задачи. 3. Метод Ритца можно использовать для решения эллиптической задачи.
Примеры.
1.
(4) определяет обобщенное решение задачи Дирихле для уравнения Пуассона.
Теорема 4.
1. Существует единственный
2. Последовательность Ритца для функционала (3) в
3.
2. Задача Неймана.
Любое решение такой задачи равно сумме частного неоднородного и общего однородного решения. Будем искать решение из
Обобщенное решение задачи (7)-(8) :
Если u=v=const, то илевая и правая части не изменятся и:
Решение существует и единственно.
Будем полагать :
Теорема 5.
1. Существует единственный
2. Последовательность Ритца для функционала (10) в
3.
Изучение классических решений эллиптических задач. §1. Формула Грина.
Вычтем из первого второе:
Интегральное представление производной. Определение. Фундаментальное решение уравнения Лапласа:
Следствие.
Теорема 1.
Пусть
Пусть
Доказательство. Рассмотрим:
Обозначим :
Надо доказать, что :
Обозначим :
где :
Учитывая, что:
Обозначим :
Первая теорема о среднем. Определение. Функция u называется гармонической в области Q , если она удовлетворяет в этой области уравнению Лапласа.
Пусть
u(x)
- гармоническая в
D
- ограниченная область
Теорема 1.
Пусть
Значение гармонической функции в центре сферы равно среднему арифметическому её значений на границе сферы. Доказательство.
Обозначим :
Вторая теорема о среднем.
Пусть
Доказательство.
Принцип максимума. Теорема.
u(x)
- гармоническая в
Q
, непрерывная в
Доказательство.
Предположим противное:
Тогда докажем, что в произвольной точке области значение функции
U
совпадает с
M
,т.е.
u
-co
nst. Возьмем
Если
Теорема доказана.
Единственность классического решения задачи Дирихле для уравнения Пуассона.
Теорема. Задача (1) (2) может иметь не более одного классического решения. Доказательство.
Предположим противное: пусть есть два классических решения:
Значит:
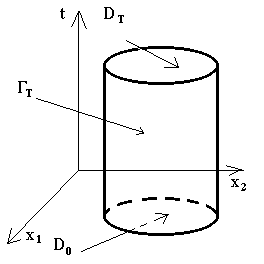
Следовательно, если существуют два решения, то они равны друг другу. Что и требовалось доказать. Обобщенные решения смешаной задачи для волнового уравнения.
Обозначения:
Умножим обе части на v и проинтегрируем по цилиндру:
Хотя обобщенное решение - общее понятие, но классическое решение может не быть обобщенным. Определение.
Обобщенное решение - функция
u
из
обобщенным решением задачи (1)-(4), если
тождество (5). Существование обобщенного решения первой смешанной задачи для волнового уравнения.
тогда:
По теореме Фубини:
Теорема.
Доказательство. Первый этап.
Пусть:
Докажем, что тогда решение u(x,t) имеет вид:
при почти всех
t
Доказано:
если
Второй этап.
то:
Третий этап. Докажем, что решения смешанной задачи со специальной правой частью сходятся к обобщенному решению. Осуществляется предельный переход:
Оценим
Докажем, что последовательность фундаментальна. Пусть N>M ; рассмотрим :
Значит
Надо доказать, что
u
- обобщенное решение, если
Единственность обобщенного решения первой смешанной задачи для волнового уравнения.
Теорема 1. Задача (1) - (4) может иметь не более одного обобщённого решения. Доказательство. Достаточно убедится, что однородная задача будет иметь единственное решение.
Возьмем:
где:
Интегральное тождество приобретет следующий вид:
Анизотропные пространства Соболева. Определение.
Анизотропным пространством Соболева
Вводится скалярное произведение:
Свойства пространств: Теорема.
Пространство
Доказательство. Фундаментальная последовательность, переход к пределу в интегральном тождестве.
Пусть
Теорема 2.
Теорема 3.
Доказательство - продолжение функции до финитной. Теорема 4.
Теорема 5.
Для
Обобщенные решения смешанной задачи для уравнения теплопроводности.
Определение.
Обобщенное решение
Существование обобщенного решения первой смешанной задачи для уравнения теплопроводности (метод Фурье, метод разделения переменных).
Будем считать:
при почти всех
t
интегрируема с квадратом в
Равенство Парсеваля:
По теореме Лебега можно слева и справа проинтегрировать по
t
и поменять местами
Решение имеет вид:
Надо доказать сходимость в
Теорема.
Доказательство. Первый этап.
Предположим, что правая часть уравнения имеет вид:
Рассмотрим:
-интегральное тождество выполняется. Второй этап.
Третий этап. Доказательство фундаментальности последовательности
Интегрируем слева и справа:
Значит: последовательность фундаментальна и она сходится:
Переходим к пределу:
Надо доказать, что u - задает решение задачи.
При переходе к пределу выполняется интегральное тождество:
Теореме доказана. Из этой теоремы не следует единственность. Единственность обобщенного решения смешанной задачи для уравнения теплопроводности.
Теорема. Задача (1)-(3) может иметь не более одного обобщенного решения. Доказательство.
Пусть
Условия, налагаемые на
v
:
Формула Кирхгофа. Дополнительные обозначения:
пусть есть
Возьмем произвольную
Обозначим:
Выберем
Обозначим через
Замечание:
Рассмотрим вспомогательную функцию:
Рассмотрим:
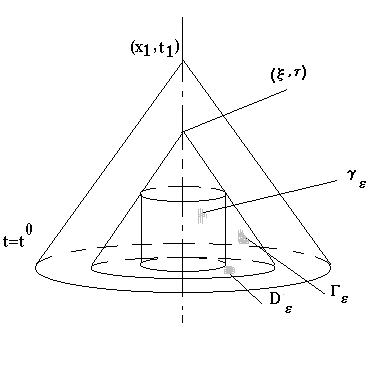
В дальнейшем: x принадлежит малому конусу с вырезанным цилиндром.
Проинтегрируем левую и правую части тождества по
где: - единичный вектор внешней нормали к границе области.
Разобьем этот интеграл на 3 интеграла:
потом
Рассмотрим на конической поверхности
Вычислим все частные производные функции
v
по
Зная, что
где:
Рассмотрим
Переход к пределу:
Вычислим:
Т.к. u - непрерывно дифференцируема на поверхности, то:
учитывая:
В силу оценки:
Получим:
Получена формула Кирхгофа: (1)
Замена переменных (чтобы легче было дифференцировать по t ):
Геометрический смысл формулы. 1. В первых двух интегралах производится интегрирование по границе основания конуса - трехмерной сфере. 2. В третьем интеграле производится интегрирование по основанию конуса - трехмерному шару. 3. Значение даламбериана вычисляется интегрированием по боковой поверхности конуса. СМЫСЛ. Дважды дифференцируемая функция u(x,t) выражается через значение первых производных на сфере (границе основания конуса) и её даламбериан на боковой поверхности конуса. Задача Коши для волнового уравнения.
Обозначим:
Определение. Функция u(x,t) , такая, что:
1)
2)
называется классическим решением задачи Коши для волнового уравнения, если:
Пусть n=3 .
Обозначим:
По формуле Кирхгофа функция
u(x,t)
выражается для любого конуса
Теорема единственности. Задача Коши (2)-(3) не может иметь более одного решения. Вопрос существования. Если классическое решение существует, то оно задается формулой Кирхгофа (4):
Таким образом, вопрос о существовании классического решения
Предварительные рассуждения.
Введем функцию:
Есть
Производится исследование
Лемма 1.
Пусть функция
g
и все её производные по пространственным переменным непрерывны до порядка
k
:
1) функция и все её производные вплоть до порядка
k
по
x
и
t
непрерывны на множестве
2) для
Доказательство.
В (5) перейдем к новой переменной, тогда:
Отсюда следует первое утверждение леммы.
Применим
Подставим
t=0
:
Возьмем производные по
t
от
Рассмотрим производную при
t=0
:
Преобразуем второе слагаемое:
обозначим :
тогда (7) примет вид:
Используем его для вычисления второй производной по времени:
Предствляя этот объемный интеграл в виде повторного интеграла: сначала по сфере, а затем от
0
до
t
, получим равенство:
Лемма доказана. Теорема 2. Пусть:
тогда: решение задачи Коши (2)-(3) существует и дается формулой Кирхгофа (4). Доказательство.
Рассмотрим второе слагаемое:
Рассмотрим первое слагаемое
Начальные условия:
Рассмотрим:
где:
В силу леммы 1
G
и все её производные по
x
и
t
до второго порядка включительно непрерывны на множестве
Функция
G
удовлетворяет:
Перейдем к
F
.
F
непрерывна вместе со всеми производными по
x
до второго порядка включительно в области
Вычислим производную
F
по
t
:
Окончательно:
Замечание. Доказательство теоремы о существовании и единственности классического решения задачи Коши в случае, когда n=3 , опиралось на интегральное представление функции в виде формулы Кирхгофа. Формулы, аналогичные формуле Кирхгофа, можно вывести для произвольного числа пространственных переменных. Эти формулы дают выражение достаточно гладкой функции u(x,t) через её первые производные и даламбериан в конусе. Пользуясь этим представлением, можно обобщить эти теоремы существования и единственности для произвольного числа переменных (n>3) . Замечание. Формулы, аналогичные формулам Кирхгофа для n=1 и n=2, можно получить из n=3 методом спуска. Метод спуска (как из формулы Кирхгофа получить формулы Пуассона и Даламбера).
Надо получить формулу Кирхгофа для n=2 - формулу Пуассона.
Обозначения:
Преобразуем интегралы:
Заменим
Получим формулу:
Получена формула Пуассона:
Формула Даламбера:
Обозначим:
Введём фундаментальное решение уравнения теплопроводности:
Свойства U для уравнения теплопроводности .
1.
2.Если
U
продолжить тождественным 0 при
Доказательство. Если выписывать производные функции U , то получится рациональная функция, умноженная на экспоненту, экспонента стремится к 0 быстрее любой рациональной функции, значит, пределы все равны 0, и получена бесконечная гладкость.
3.
Доказательство.
В качестве упражнения:
4.
где
Дополнительные обозначения.
Пусть
Введём
n
- размерность постранства
N - определяет область интегрирования. Будем считать:
Сначала рассмотрим интеграл:
Можно применить теорему Лебега о предельном переходе под знаком интеграла:
Т.к.
произведём замену
Если докажем, что остальные пределы дают 0. Формула Пуассона:
Можно найти решение задачи Коши для уравнения теплопроводности: Рассматривается задача:
Если решение из рассматриваемого класса существует, то оно представляется формулой:
В рассматриваемом классе решений задача Коши для уравнения теплопроводности может иметь не более 1 решения.
Применим теорему Лебега о предельном переходе под знаком интеграла (необходимо, чтобы все элементы последовательности были ограничены интегральной функцией).
где :
Подынтегральная функция ограничена .
Так как :
Замена :
Сделано ограничение интегрируемой функцией. Можно применять теорему Лебега о предельном переходе. Теория Фредгольма. (в Гильбертовом или Банаховом пространстве).
Рассмотрим компактный оператор
Изучаем уравнение :
однородное уравнение
однородное сопряженное уравнение
Теорема Фредгольма. Теорема. 1. Если однородное уравнение (2) имеет единственное тривиальное решение, то неоднородное уравнение (1) имеет единственное решение для любой правой части из гильбертова пространства H.
2. Если уравнение (2) имеет нетривиальное решение, то тогда неоднородное уравнение (1) разрешимо тогда и только тогда, когда правая часть уравнения (1) ортогональна всем решениям уравнения (3) :
3. Размерность ядра оператора
Введём :
Лемма 1.
Доказательство.
Предположим противное :
Ядро - замыкает линейное подпространство.
Следовательно единичный шар отображается на себя (в некомпактное множество), а оператор компактный. Ядро - замыкание бесконечномерного подпространства Гильбертова пространства. Имеем противоречие, доказывающее теорему. Лемма 2.
Доказательство.
Пусть
Разложим
Значит :
1).
Тогда :
2).
Из сходимости следует, что ненулевые элементы принадлежат ядру и ортогональному дополнению :
Лемма 3.
Доказательство. (первая часть)
Пусть
Получили :
Пусть
Значит :
Введём обозначения :
Лемма 4.
Доказательство. Предположим противное : пусть такого k не существует.
Возьмём n<m и рассмотрим
При этом
Из подпоследовательности
Получили противоречие. Лемма 5.
Пусть
Доказательство. (совпадает с доказательством 1-ой части теоремы).
Предположим противное :
Предположили :
Для
Одновременно : для
Пусть
По индукции :
Получено противоречие. Лемма 5 доказана. Лемма 6.
Доказательство.
Предположим противное, т.е.
Обозначим через
Если докажем, что оператор S имеет тривиальное ядро, то по лемме 5 получим :
Пусть
Если x ортогонален
Можно выбрать
Умножим левую и правую части равенства на
Значит : n=m. Доказательство теоремы Фредгольма. 1) доказано по лемме 5 ; 2) доказано по лемме 6 и по лемме 3; 3) доказано по лемме 1 и 6. Теорема доказана.
Тема. Теорема Гильберта-Шмидта.
Пусть
Лемма 1.
Пусть
Доказательство.
Пусть
Лемма 2.
Пусть
Доказательство.
Пусть
Значит, собственные функции ортогональны. Дополнительные обозначения.
Рассмотрим квадратичную форму
Лемма 3.
Пояснение:
т.е.
Доказательство.
1) докажем, что:
2) докажем, что:
Лемма доказана.
Обозначим через
Лемма 4.
Пусть
Доказательство. Вместо A рассмотрим A-mE (спектр сдвинется на m, и оператор станет неотрицательным):
Не ограничивая общности рассуждений: оператор A - неотрицательный.
2.
Получено:
A-ME - не может иметь ограниченный обратный оператор. Определение.
Подпространство
Лемма 5.
Пусть
Доказательство.
Пусть
Рассмотрим:
Лемма доказана. Лемма 6. Спектр компактного, самосопряженного оператора состоит из 0 и изолированных собственных значений конечной кратности. Доказательство.
1. Докажем, что
Пусть
Возьмем
2. Рассмотрим
Если
Случай 1: (2) имеет нетривиальное решение, и (1) имеет решение не для всех правых частей, а только для тех, которые ортогональны решениям (2).
Случай 2:
3. Докажем: все собственные значения ограничены.
Рассмотрим
тогда:
Получено противоречие.
Комментарии:
- 0 может быть собственным значением бесконечной кратности, а остальная часть спектра - из конечного числа собственных значений. - 0 может не быть собственным значением, но тогда он - точка непрерывного спектра. Окончательно: спектр состоит из изолированных собственных значений конечной кратности и 0. Теорема Гильберта-Шмидта.
Пусть
Доказательство.
Оператор
A
- ненулевой, следовательно:
Значит,
Проведем процесс ортогонализации, и получим
Конец:
на каком-то ортогональном подпространстве оператор
A
обращается в 0, и получена конечная сумма , т.е.
иначе:
Возможны 2 случая: 1) ортонормированный базис из элементов подпространств ( в этом случае система собственных векторов дополнняется до ортонормированного базиса элементами ядра оператора A):
2) бесконечный ортонормированный базис :
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
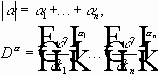 - дифференциальный оператор.
- дифференциальный оператор.
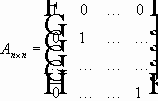

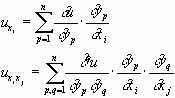
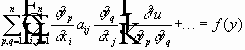 (1')
(1')
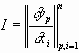 .
.
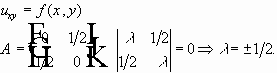
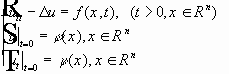
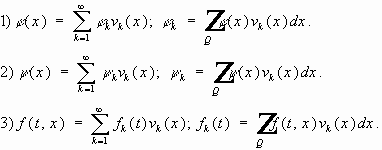
 (8)
(8)
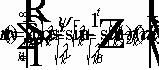 (9)
(9)
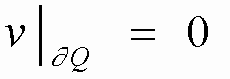
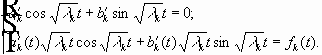 (10)
(10)
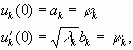
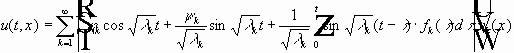
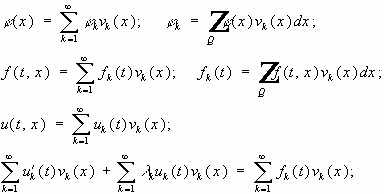

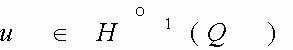


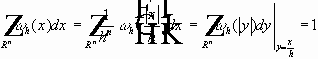 ,
С
находится из условия
,
С
находится из условия

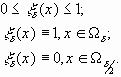

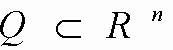
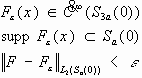
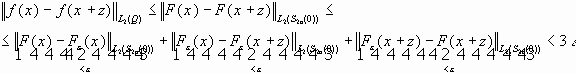

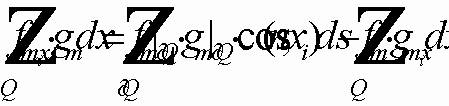


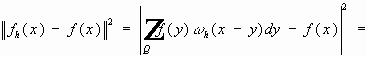
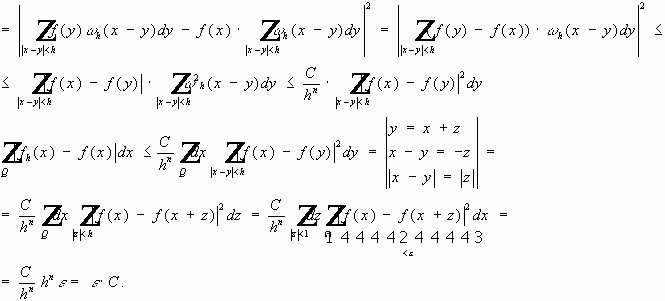

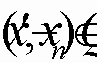

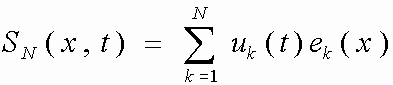
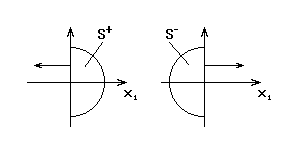
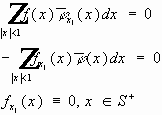
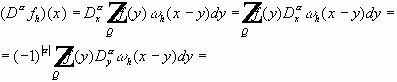
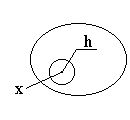
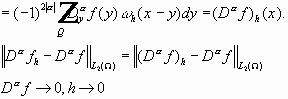
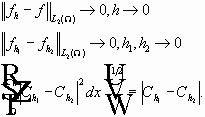
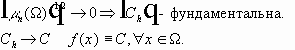
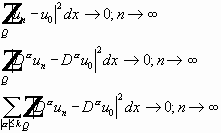

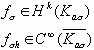
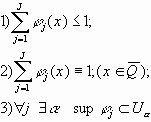
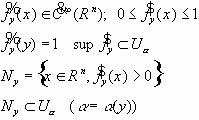
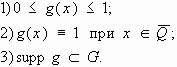
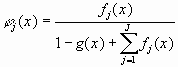 .
.
 выполняется свойство 3.
выполняется свойство 3.
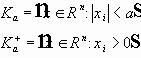
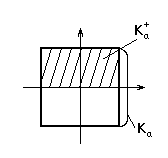
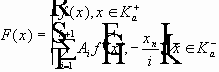 (2)
(2)

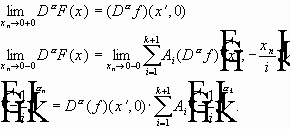
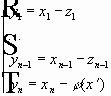 - невырожденное преобразование координат.
- невырожденное преобразование координат.
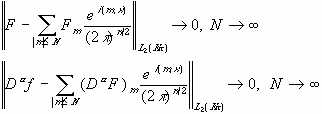
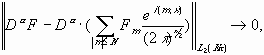 и следовательно :
и следовательно :
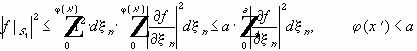
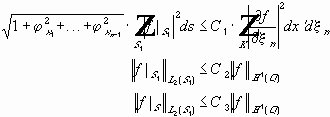
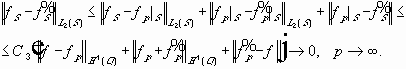
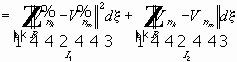
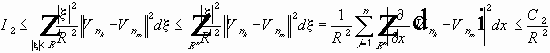
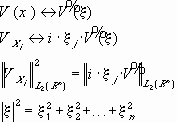
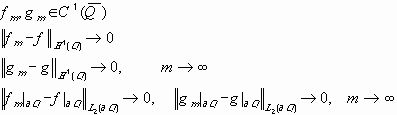
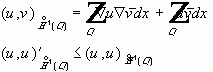


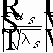 составляет ортонормированный базис в
составляет ортонормированный базис в
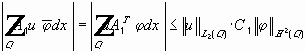
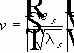 в
в
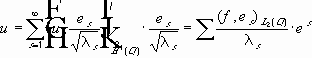

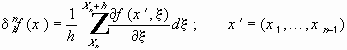 (3)
(3)
 (4)
(4)
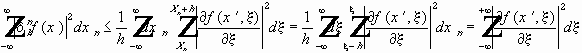

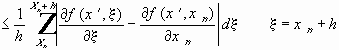
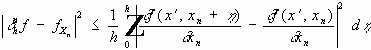

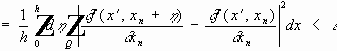
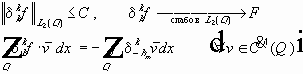

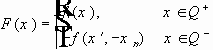
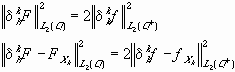
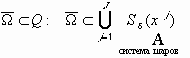
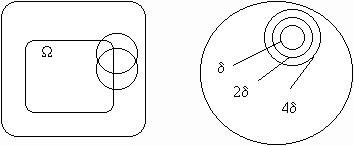
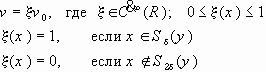
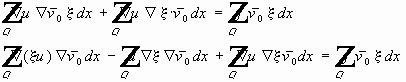
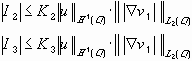
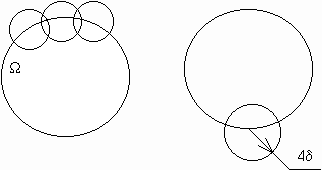
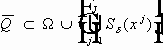
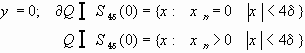
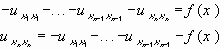
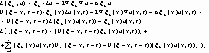 ,
,
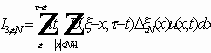 .
.
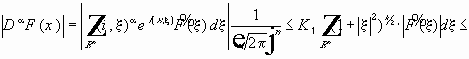
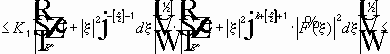
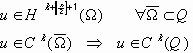

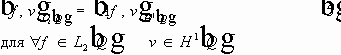
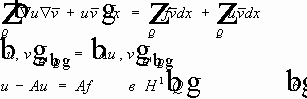
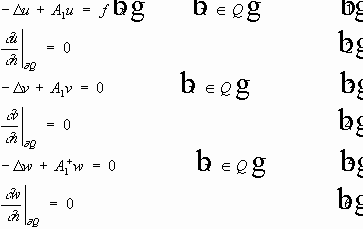

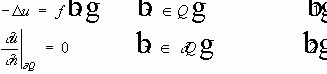
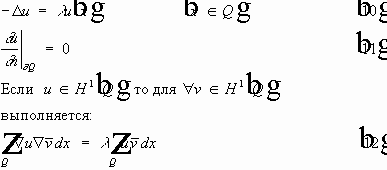 Теорема 3.
Теорема 3.
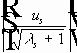 составляют ортонормированный базис в
составляют ортонормированный базис в
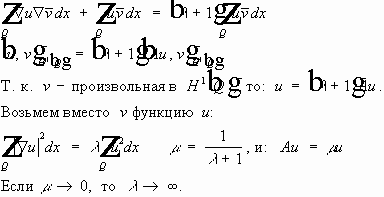
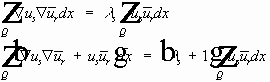
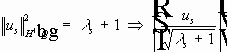 - ортонормированный базис в
- ортонормированный базис в

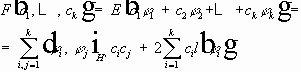
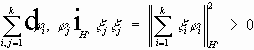
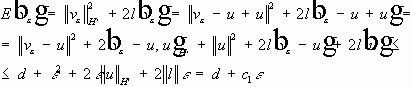
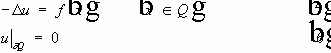
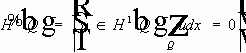 - замкнутое подпространство пространства
- замкнутое подпространство пространства
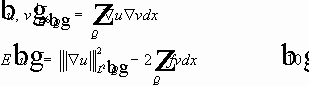
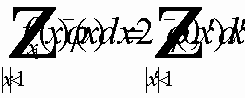
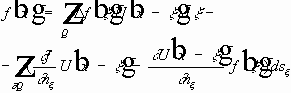
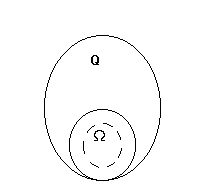
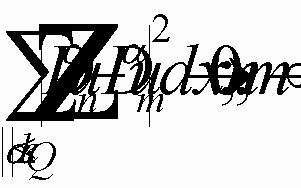 -- область без шара.
-- область без шара.



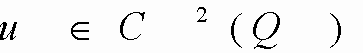
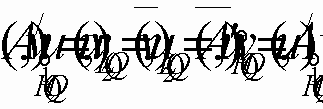
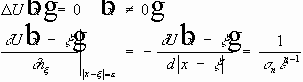
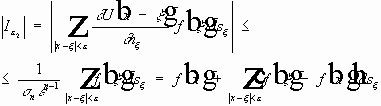
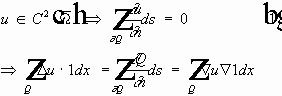
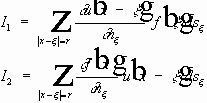
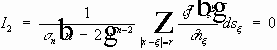
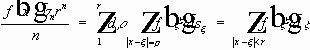
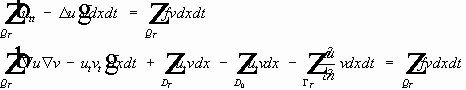
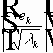 - базис,
- базис,
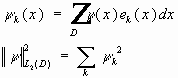
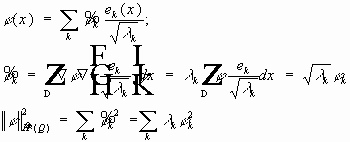
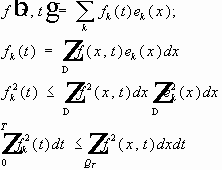
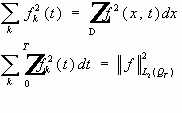

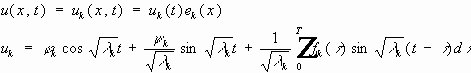
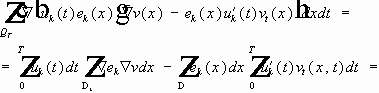
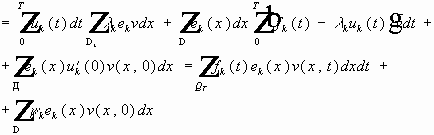
 , то:
, то:
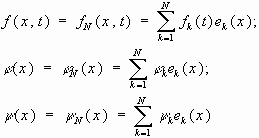
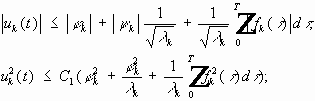
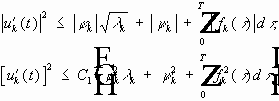

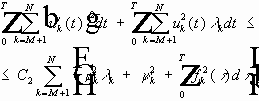
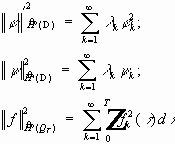

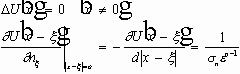

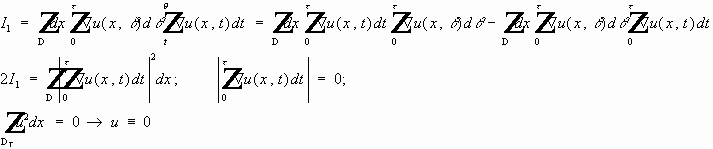 Теорема доказана.
Теорема доказана.
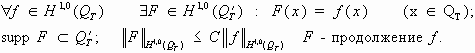
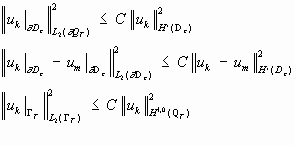
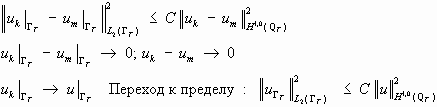
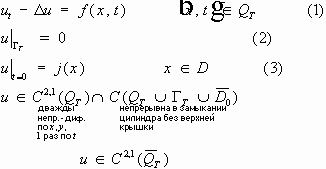
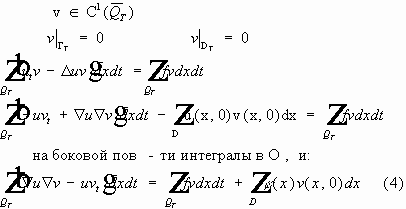
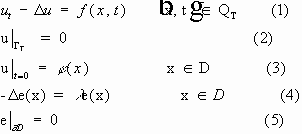
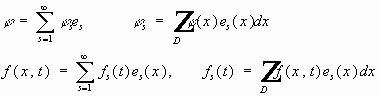

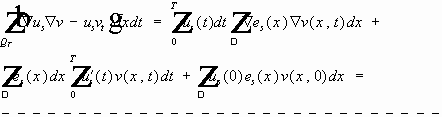
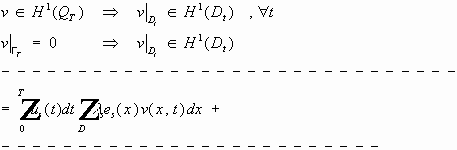


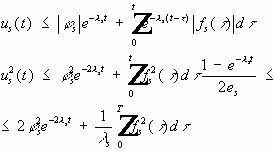
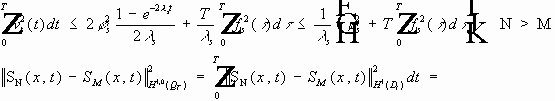
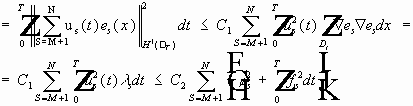
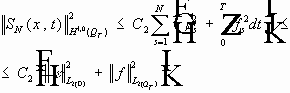
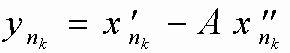
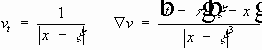
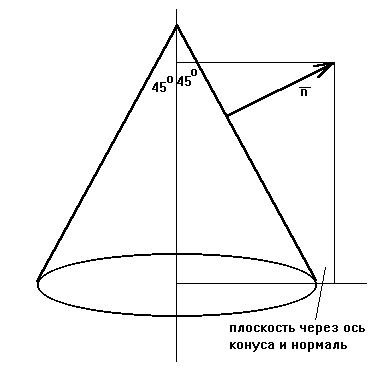
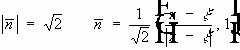
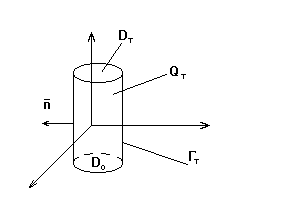
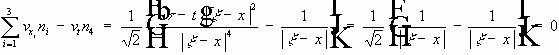 ,
,
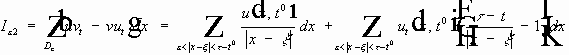
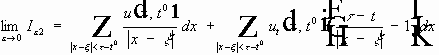
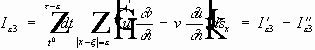
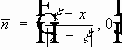 - внутренняя нормаль к цилиндру.
- внутренняя нормаль к цилиндру.


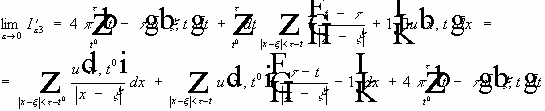

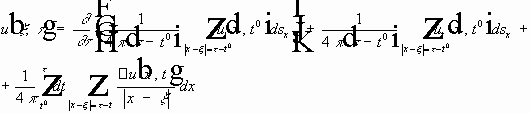
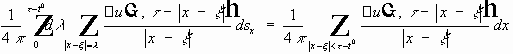
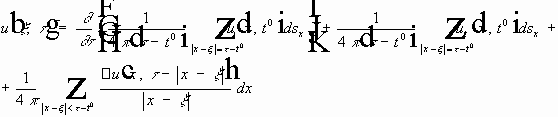
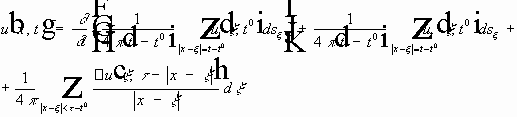
 Продифференцировано первое слагаемое:
Продифференцировано первое слагаемое:
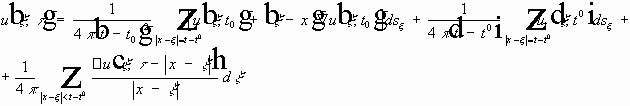
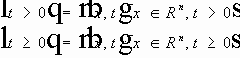
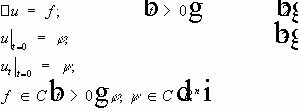
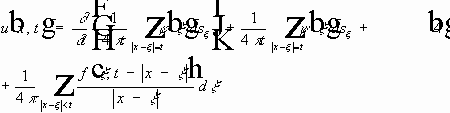
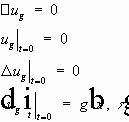
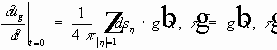
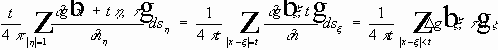
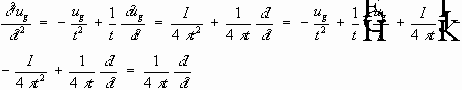
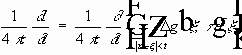
 - вследствие формулы (6) справедливо последнее равенство.
- вследствие формулы (6) справедливо последнее равенство.
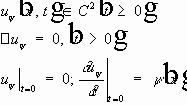
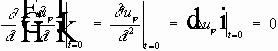 .
.
 ,
,
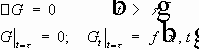
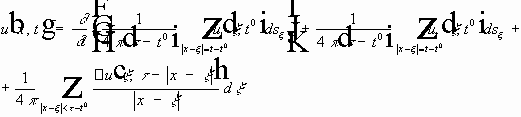
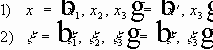

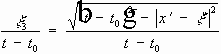 Рассмотрим:
Рассмотрим:
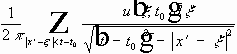
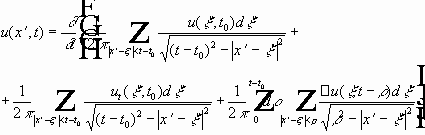
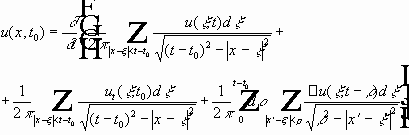

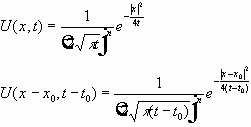

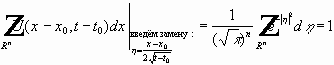

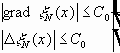 - используются срезающие функции.
- используются срезающие функции.
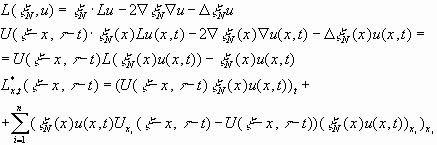

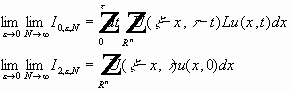

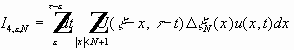
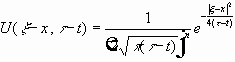 , то :
, то :
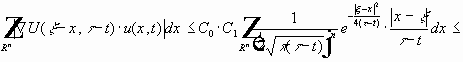
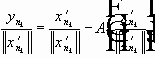 ,
,
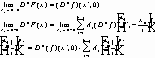 .
.
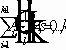 ,
,

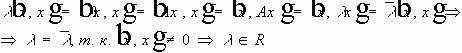
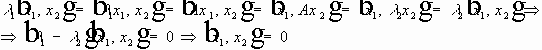
 ,
,

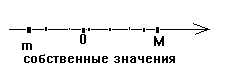
 Главная
Главная